R4CR

Day2 - 생존분석 심화 | 2023-06-15
Jinseob Kim

요약

• 자체 개발한 jskm 패키지로 kaplan-meier 그림을 그린다.

• Log-log plot, Observed-expected plot 으로 비례위험가정을 확인 후, cox.zph 함수로 p-value 를 구한다.

• anova로 여러 모형의 log-likelohood 를 비교하고, step으로 AIC 기반 최적모형을 고를 수 있다.

• Time-dependent analysis 는 (1) 비례위험가정이 깨졌을 때, (2) 반복측정 공변량이 있을 때 수행한다.

• 모수적 생존분석은 생존함수 \(S(t)\) 를 구할 수 있어 예측모형을 만들 수 있다.

Kaplan-meier plot

• Kaplan-meier plot 은 R 기본 plot에서도 제공하지만, survminer 패키지의 ggsurvplot 함수에서 다양한 옵션을 제공한다.

• 본 실습에서는 본사가 개발한 jskm 패키지의 jskm 함수를 survival 패키지 내장 데이터 veteran 에 적용하겠다.

surv dataset +

• 우선 패키지를 불러온 후 survfit 으로 구간별 생존율을 구하자.

library(DT)
library(survival)
library(jskm)
datatable(veteran, rownames = F, caption = "Example data", options = list(scrollX = T))

surv object

sfit <- survfit(Surv(time, status) ~ trt, data = veteran)
summary(sfit, times = c(100, 200, 300, 365), extend = T)

Call: survfit(formula = Surv(time, status) ~ trt, data = veteran)

                trt=1 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
  100     34      34   0.5020  0.0606       0.3962        0.636
  200     12      19   0.1947  0.0501       0.1176        0.322
  300      5       6   0.0885  0.0371       0.0390        0.201
  365      4       1   0.0708  0.0336       0.0279        0.180

                trt=2 
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
  100     21      45    0.333  0.0578       0.2367        0.467
  200     13       7    0.216  0.0517       0.1354        0.345
  300      8       4    0.146  0.0454       0.0797        0.269
  365      6       2    0.110  0.0407       0.0530        0.227

jskm

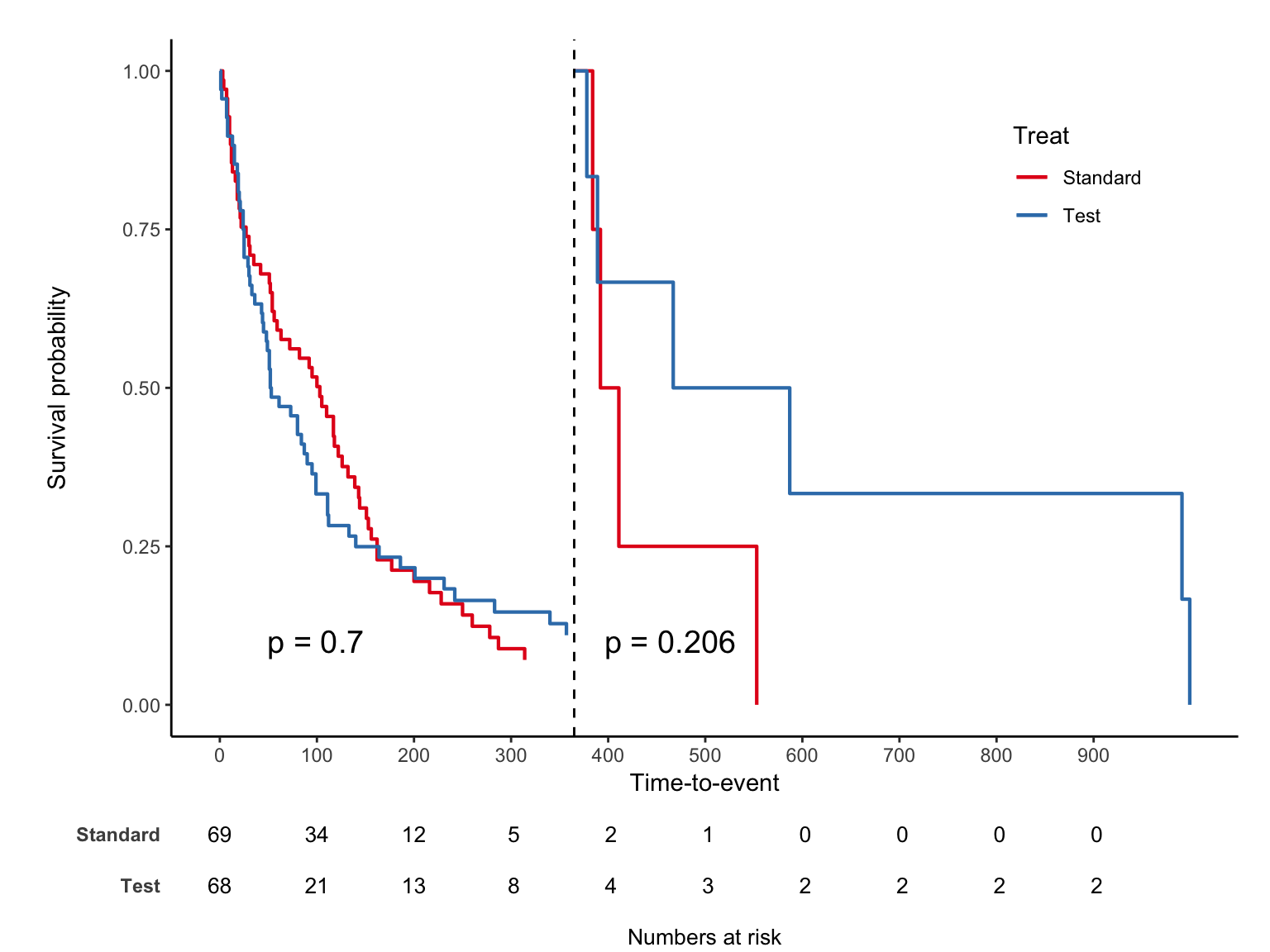
trt 1 은 “Standard”, 2 는 “Test” 이며 jskm 을 적용하면 아래와 같다.

jskm(sfit)

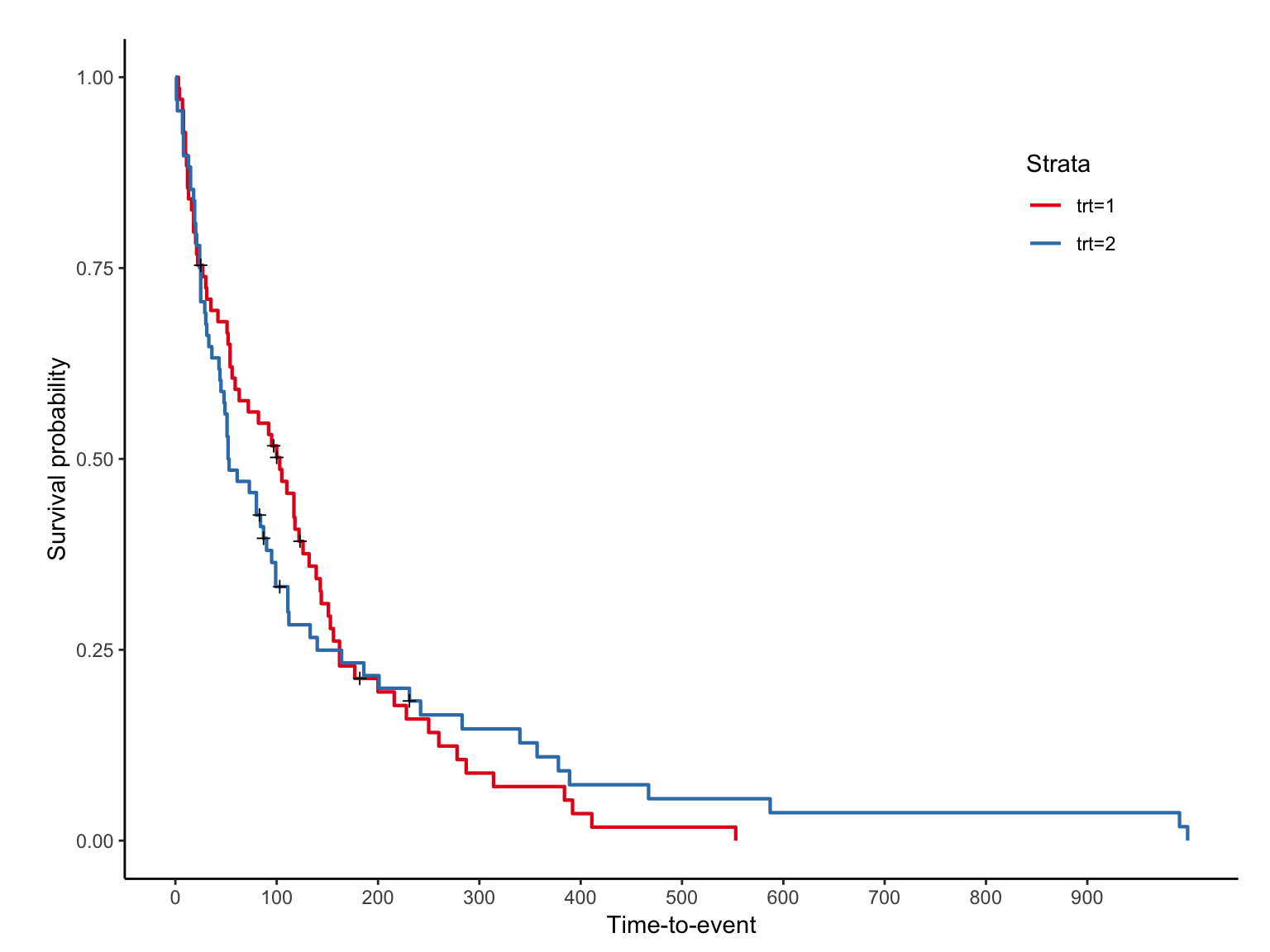
label, table, pvalue

라벨을 수정하고, risk table 과 log-rank p-value 를 추가하자.

jskm(
  sfit, 
  ystrataname = "Treat", 
  ystratalabs = c("Standard", "Test"), 
  table = T, pval = T
)

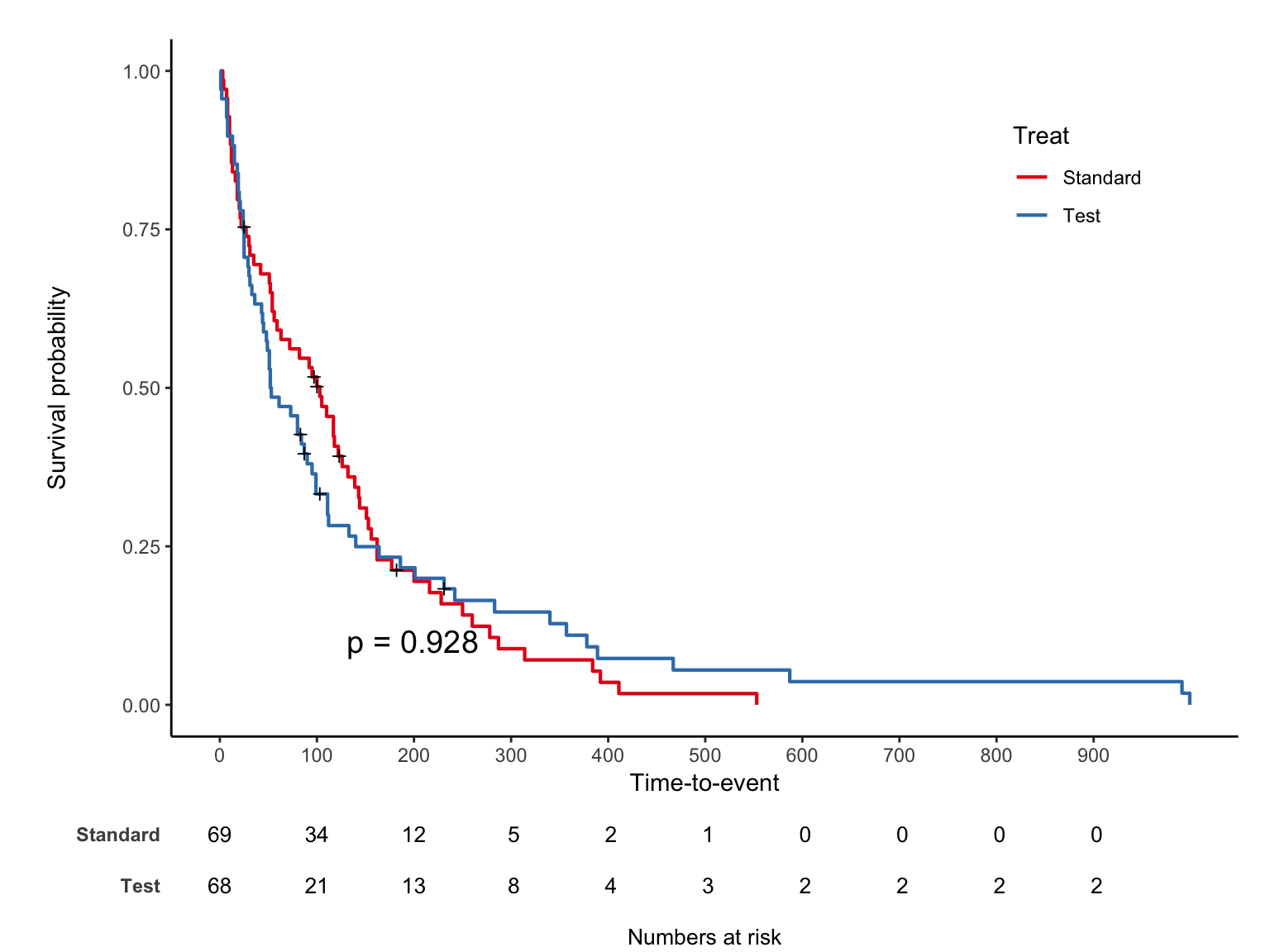
십자가 무늬는 실제 censoring이 발생한 부분이며 mark = F로 숨길 수 있다.

cumulative

생존율이 아닌 누적발생률을 %로 보는 코드는 아래와 같다.

jskm(
  sfit, 
  ystrataname = "Treat", 
  ystratalabs = c("Standard", "Test"), 
  table = T, pval = T, 
  marks = F, cumhaz = T, 
  surv.scale = "percent" 
)

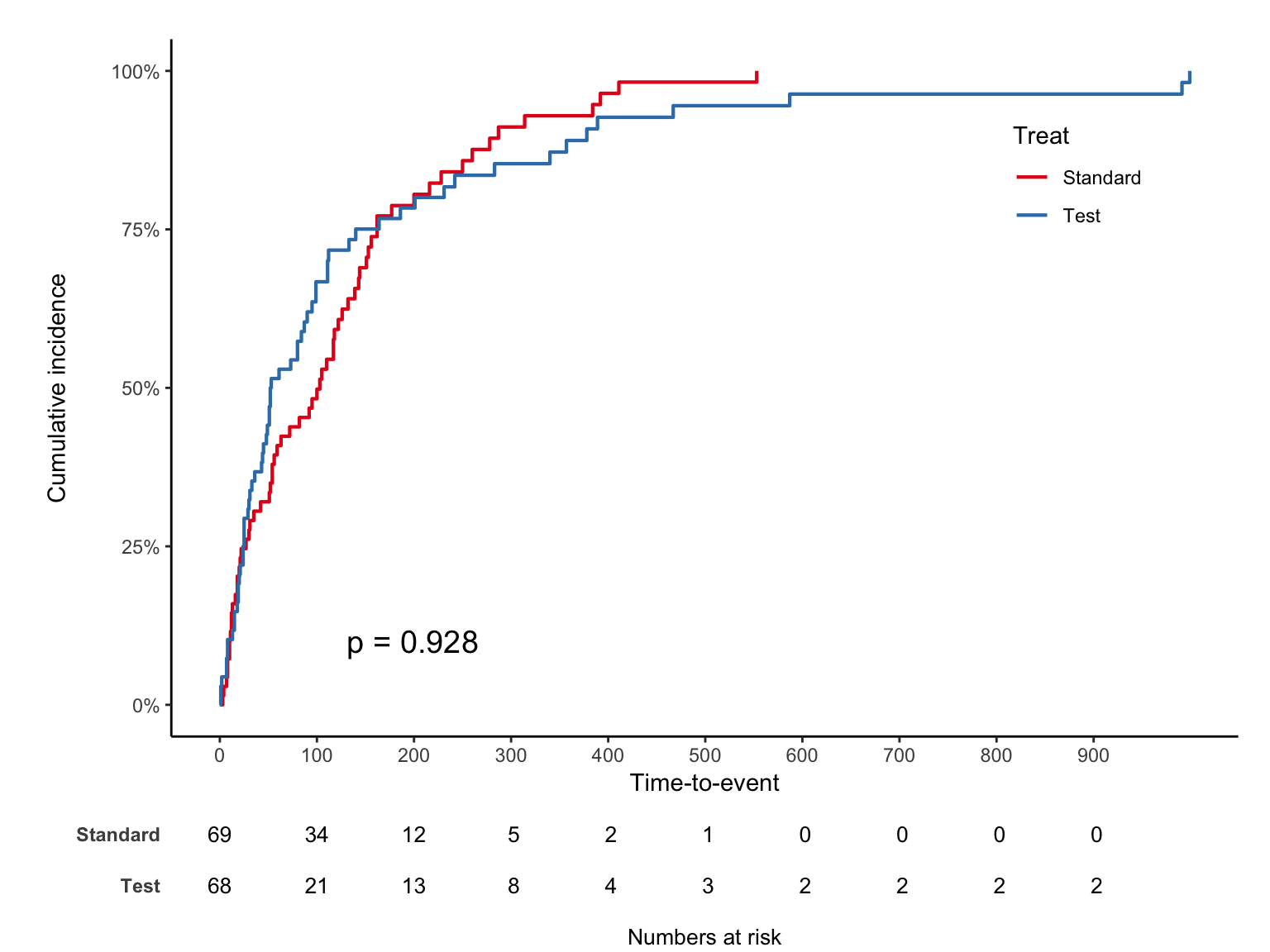
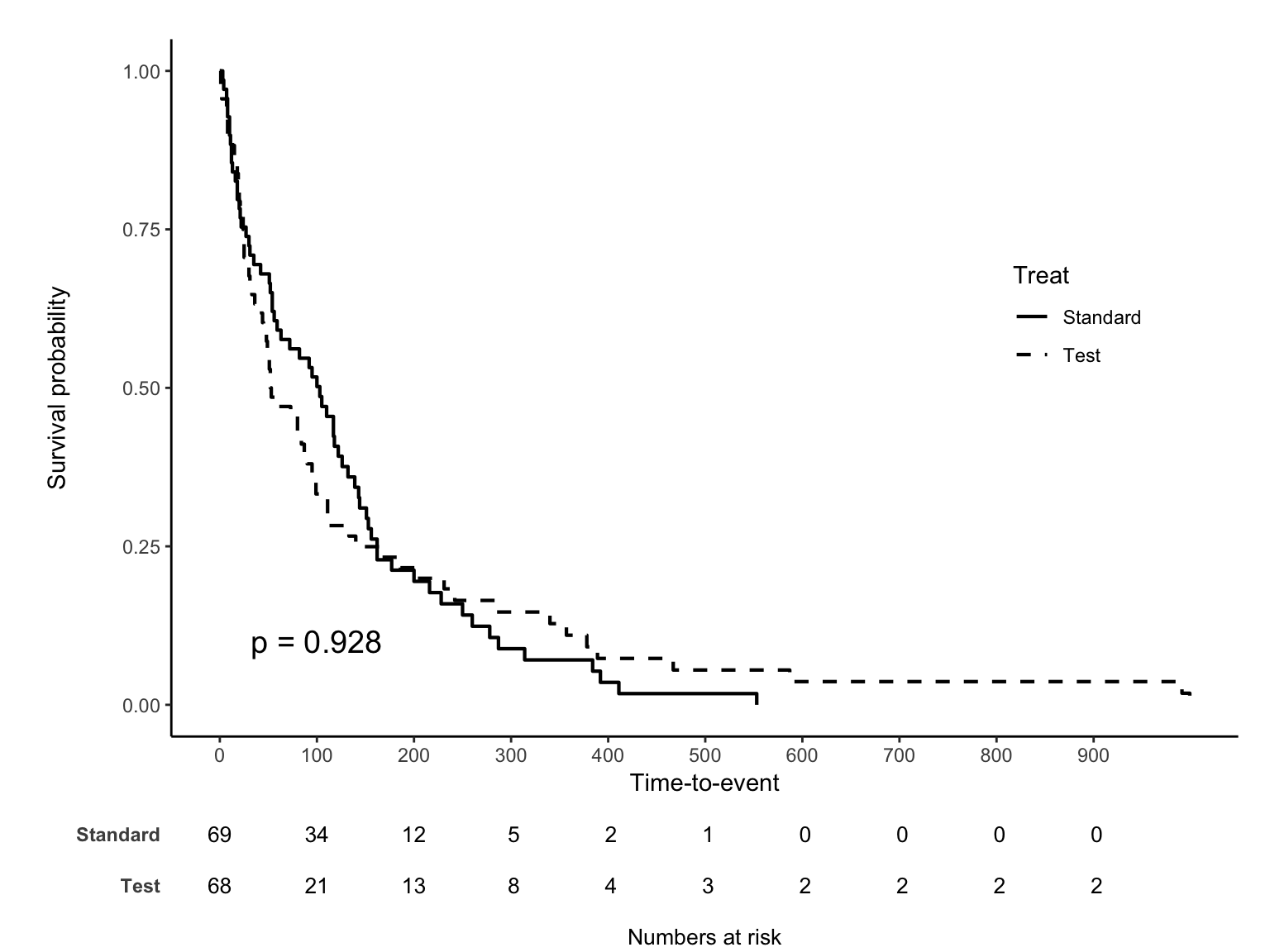
p-value 위치는 pval.coord legend 위치는 legendposition 옵션을 이용한다. 선을 흑백으로 바꾸려면 linecols = "black" 을 추가한다. legendposition 은 x,y 값 모두 0~1 scale 임을 주의하자.

legend

jskm(
  sfit, 
  ystrataname = "Treat", 
  ystratalabs = c("Standard", "Test"), 
  table = T, pval = T, 
  marks = F, pval.coord = c(100, 0.1), 
  legendposition = c(0.85, 0.6), linecols = "black"
)

landmark analysis

마지막으로 특정 시간을 기준으로 나누어보는 landmark analysis 옵션을 소개한다.

jskm(
  sfit, 
  ystrataname = "Treat", 
  ystratalabs = c("Standard", "Test"), 
  table = T, pval = T, 
  marks = F, 
  cut.landmark = 365
)

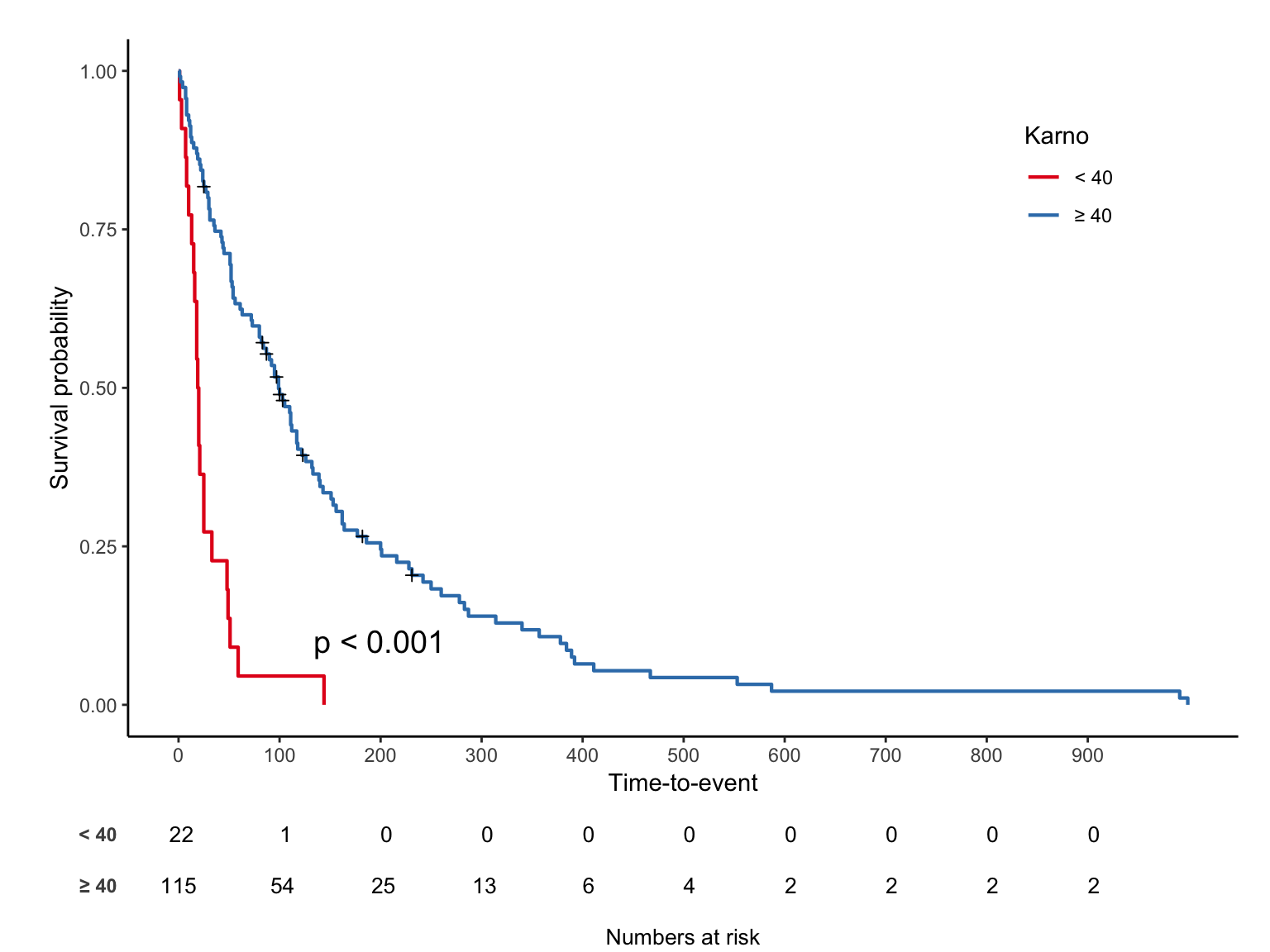
연속변수의 최적 cut-off 구하기

maxstat 패키지를 이용한다.

library(maxstat)
mtest <- maxstat.test(
  Surv(time, status) ~ karno, 
  data = veteran, 
  smethod = "LogRank"
)

mtest

Maximally selected LogRank statistics using none

data:  Surv(time, status) by karno
M = 4.6181, p-value = NA
sample estimates:
estimated cutpoint 
                40 

plot

cut <- mtest$estimate
veteran$karno_cat <- factor(as.integer(veteran$karno >= cut))

sfit2 <- survfit(Surv(time, status) ~ karno_cat, data = veteran)
jskm(sfit2, ystrataname = "Karno", ystratalabs = paste(c("<", "≥"), cut), table = T, pval = T)

비례위험가정 확인

Logrank test, Cox model로 추정할 때 비례위험을 가정하므로 이것이 깨지면 큰일이다.

본 글에서는 비례위험가정을 확인하는 그림 2개와 테스트를 소개한다.

자세한 내용은 외부 링크를 참고하기 바란다.

Log-log plot

plot(
  sfit, fun = "cloglog",
  lty = 1:2, col = c("Black", "Grey50"), lwd = 2,
  font.lab = 2, main ="Log-log KM curves by Treat",
  xlab = "Time (log scale)", ylab = "log-log survival"
)

legend("bottomright", lty = 1:2, legend = c("Standard", "Test"), bty = "n", 
       lwd = 2, col = c("Black", "Grey50"))

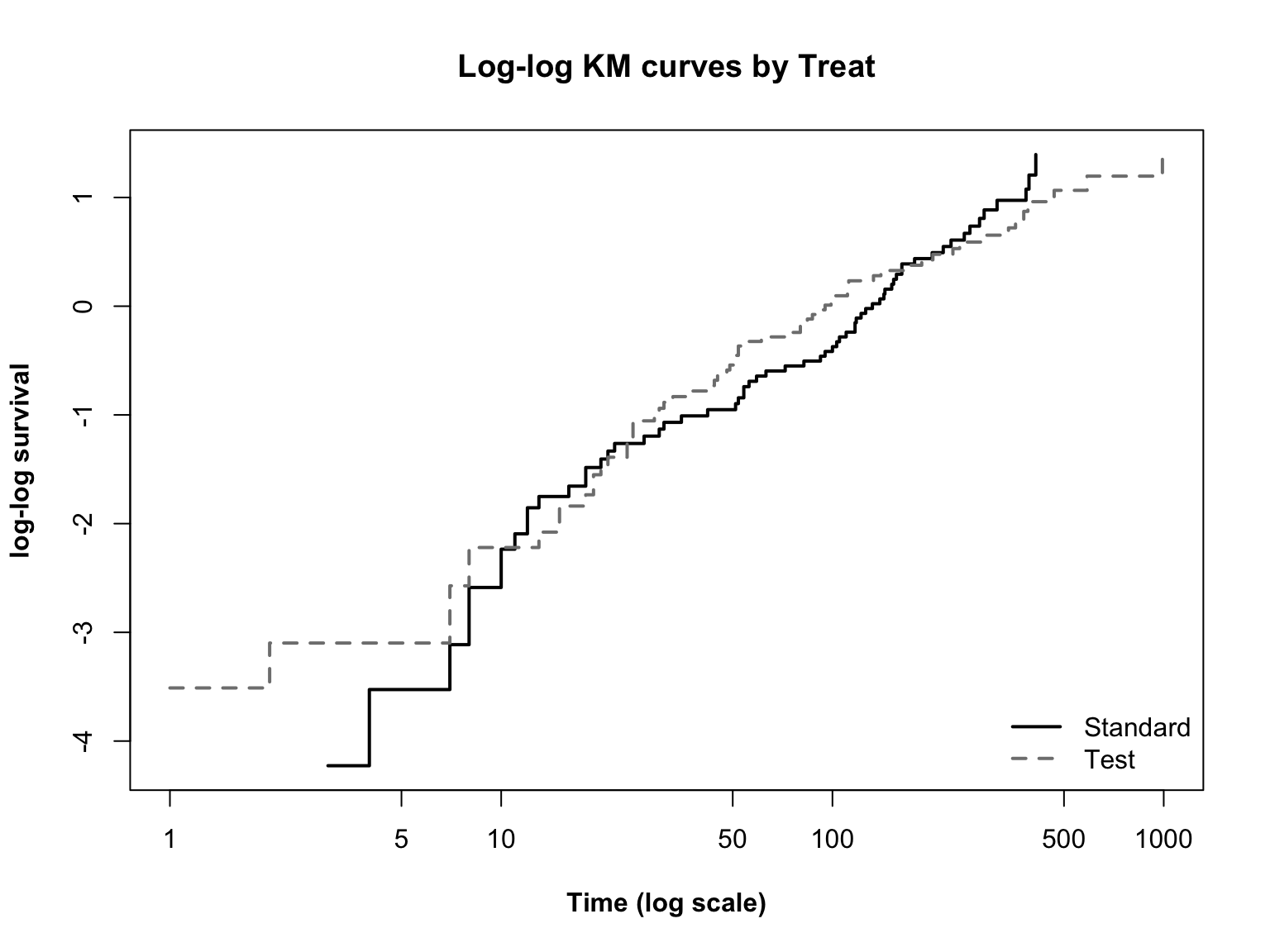
Log-log plot 2

\(\log(t)\) 와 \(\log(-\log(S(t)))\) 관계를 그림으로 보는 방법이다.

왜 로그를 이용하는지는 모수적 생존분석에서 이야기하겠다.

두 선이 평행한지 확인하면 되고 직선인지 곡선인지는 상관없다.

모수적 생존분석에서 다룰 weibull 모형에서는 직선인지도 확인해야 한다.

Observed-expected plot

plot(
  sfit, lty = "dashed", col = c("Black", "Grey50"), lwd = 2, font = 2, 
  font.lab = 2, main = "Observed Versus Expected Plots by Treat", 
  xlab = "Time", ylab = "Survival probability")
par(new = T)

#expected
exp <- coxph(Surv(time, status) ~ trt, data = veteran)
new_df <- data.frame(trt = c(1, 2))
kmfit.exp <- survfit(exp, newdata = new_df)
plot(kmfit.exp, lty = "solid", col = c("Blue", "Red"), lwd =2, font.lab = 2)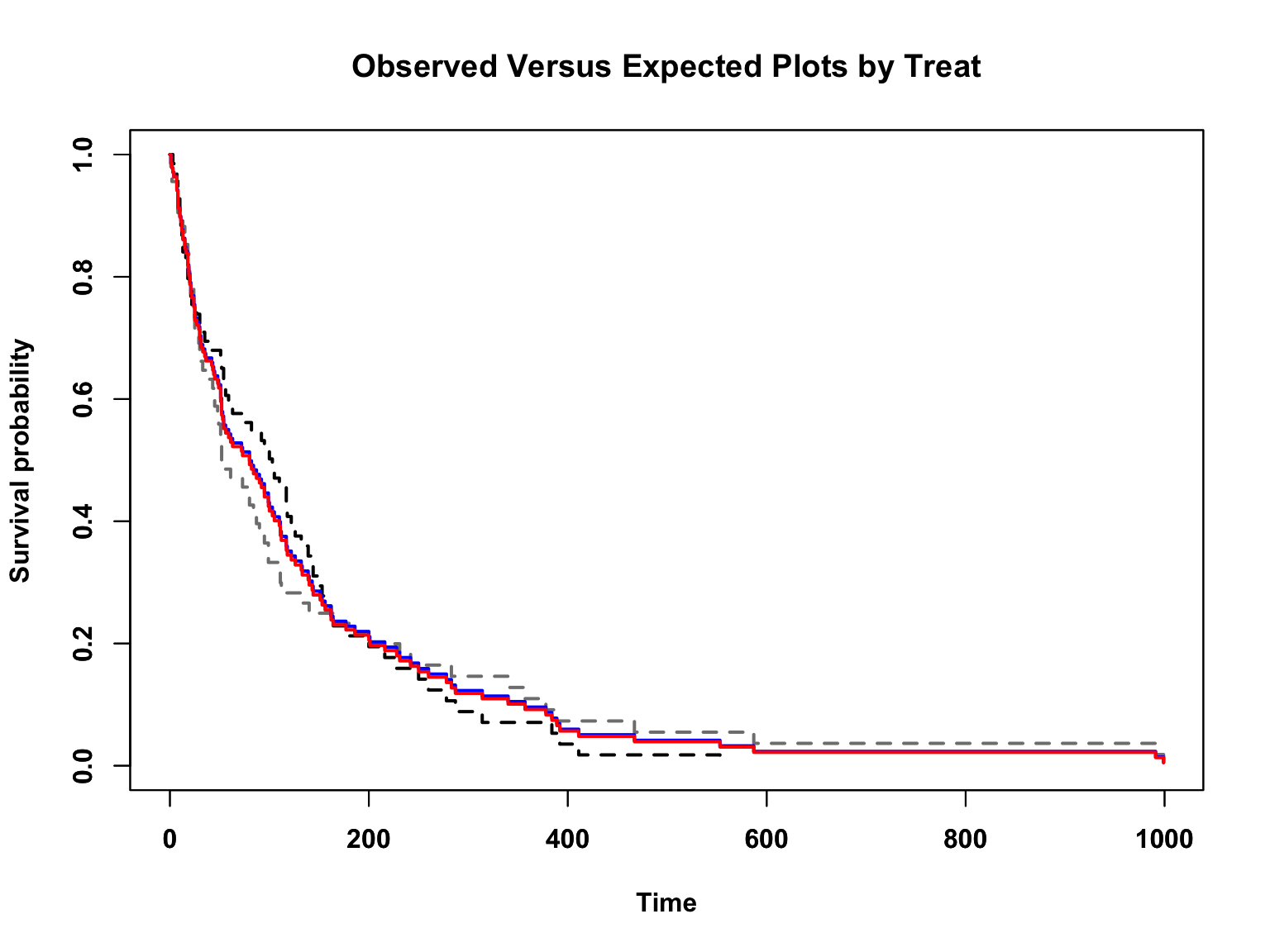

비례위험을 가정하는 cox model 예상과 비교하는 방법이다.

Goodness of fit

cox.zph 함수로 통계검정을 수행한다.

cox.zph(exp)

       chisq df    p
trt     3.54  1 0.06
GLOBAL  3.54  1 0.06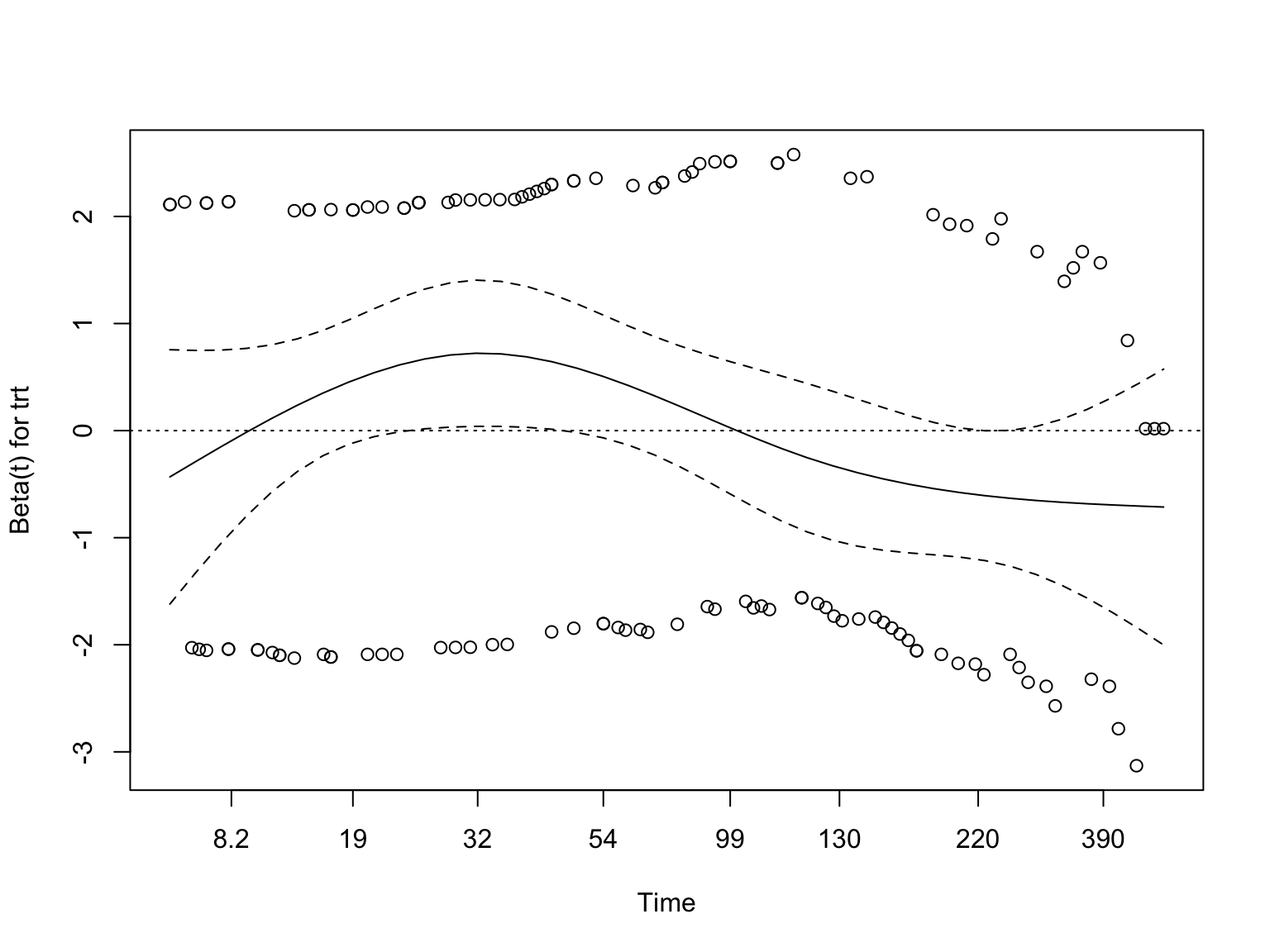

plot(cox.zph(exp), var = "trt")
abline(h = 0, lty = 3)

선이 시간 상관없이 일정할수록, 즉 x축과 평행할수록 비례위험가정을 만족한다고 판단한다. 위 그림은 x축과 평행은 아니지만 경향성이 있다고 볼수도 없는 애매한 느낌이며 p 는 0.06 이다.

모형 비교

Cox 모형에서 얻은 log-likelihood 값으로 여러 모형을 비교할 수 있다. 모형들은 n수가 전부 동일 해야 비교 가능하므로, 에러 나올땐 먼저 결측치를 확인하자.

exp$loglik

[1] -505.4491 -505.4442

모형 비교 2

exp2 <- coxph(Surv(time, status) ~ trt + age, data = veteran)
exp3 <- coxph(Surv(time, status) ~ trt + age + celltype, data = veteran)

anova(exp, exp2, exp3)

Analysis of Deviance Table
 Cox model: response is  Surv(time, status)
 Model 1: ~ trt
 Model 2: ~ trt + age
 Model 3: ~ trt + age + celltype
   loglik   Chisq Df Pr(>|Chi|)    
1 -505.44                          
2 -505.14  0.6162  1     0.4325    
3 -492.43 25.4161  3  1.264e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

최적모형 +

step 함수를 이용, AIC 기반 최적 모형을 고를 수 있다. scope 옵션으로 빠지면 안 될 변수를 미리 정한다.

step(exp3, scope = list(lower = ~ 1))

Start:  AIC=994.86
Surv(time, status) ~ trt + age + celltype

           Df     AIC
- age       1  993.04
- trt       1  993.65
<none>         994.86
- celltype  3 1014.27

Step:  AIC=993.04
Surv(time, status) ~ trt + celltype

           Df     AIC
- trt       1  992.05
<none>         993.04
- celltype  3 1012.89

Step:  AIC=992.05
Surv(time, status) ~ celltype

           Df     AIC
<none>         992.05
- celltype  3 1010.90

Call:
coxph(formula = Surv(time, status) ~ celltype, data = veteran)

                    coef exp(coef) se(coef)     z        p
celltypesmallcell 1.0013    2.7217   0.2535 3.950 7.83e-05
celltypeadeno     1.1477    3.1510   0.2929 3.919 8.90e-05
celltypelarge     0.2301    1.2588   0.2773 0.830    0.407

Likelihood ratio test=24.85  on 3 df, p=1.661e-05
n= 137, number of events= 128 

Time-dependent analysis

자세한 내용은 용어 - timedep를 참고하기 바란다.

비례위험가정 깨졌을 때 (time-dependent coefficients)

어떤 공변량이 비례위험가정을 만족하지 않을 경우, 먼저 survSplit 으로 time 을 쪼개 몇 개의 그룹으로 나눈다.

vet2 <- survSplit(
  Surv(time, status) ~ ., data = veteran, cut = c(90, 180), 
  episode = "tgroup", id = "id")

Time-dependent analysis 2

이제 공변량의 계수를 시간그룹 별로 따로 구한다.

vfit2 <- coxph(
  Surv(tstart, time, status) ~ trt + prior + karno:strata(tgroup), 
  data = vet2
)
summary(vfit2)

Call:
coxph(formula = Surv(tstart, time, status) ~ trt + prior + karno:strata(tgroup), 
    data = vet2)

  n= 225, number of events= 128 

                                  coef exp(coef)  se(coef)      z Pr(>|z|)    
trt                          -0.011025  0.989035  0.189062 -0.058    0.953    
prior                        -0.006107  0.993912  0.020355 -0.300    0.764    
karno:strata(tgroup)tgroup=1 -0.048755  0.952414  0.006222 -7.836 4.64e-15 ***
karno:strata(tgroup)tgroup=2  0.008050  1.008083  0.012823  0.628    0.530    
karno:strata(tgroup)tgroup=3 -0.008349  0.991686  0.014620 -0.571    0.568    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

                             exp(coef) exp(-coef) lower .95 upper .95
trt                             0.9890      1.011    0.6828    1.4327
prior                           0.9939      1.006    0.9550    1.0344
karno:strata(tgroup)tgroup=1    0.9524      1.050    0.9409    0.9641
karno:strata(tgroup)tgroup=2    1.0081      0.992    0.9831    1.0337
karno:strata(tgroup)tgroup=3    0.9917      1.008    0.9637    1.0205

Concordance= 0.725  (se = 0.024 )
Likelihood ratio test= 63.04  on 5 df,   p=3e-12
Wald test            = 63.7  on 5 df,   p=2e-12
Score (logrank) test = 71.33  on 5 df,   p=5e-14

반복측정 공변량이 있을 때

Ann Transl Med 2018;6(7):121 예제를 이용하였다.

library(survsim)
N <- 100 #number of patients
set.seed(123)
df.tf <- simple.surv.sim(#baseline time fixed
 n = N, foltime = 500,
 dist.ev = c('llogistic'),
 anc.ev = c(0.68), beta0.ev = c(5.8),
 anc.cens = 1.2, beta0.cens = 7.4,
 z = list(c("unif", 0.8, 1.2)), beta = list(c(-0.4),c(0)),
 x = list(c("bern", 0.5), c("normal", 70, 13))
)

for (v in 4:7){
  df.tf[[v]] <- round(df.tf[[v]])
}

names(df.tf)[c(1, 4, 6, 7)]<-c("id", "time", "grp", "age")
df.tf <- df.tf[, -3]

datatable(df.tf, rownames = F, caption = "df.tf: Original data", options = list(scrollX = T))

cont.

nft <- sample(1:10, N, replace = T) #number of follow up time points
crp <- round(abs(rnorm(sum(nft) + N, mean = 100, sd = 40)), 1)
time <- NA
id <- NA
i <- 0
for(n in nft){
  i <- i+1
  time.n <- sample(1:500, n)
  time.n <- c(0, sort(time.n))
  time <- c(time, time.n)
  id.n <- rep(i, n+1)
  id <- c(id, id.n)
}
df.td <- cbind(data.frame(id,time)[-1,], crp)
datatable(df.td, rownames = F, caption = "df.td: Time dependent CRP", options = list(scrollX = T))

tmerge

df.tf 는 기본정보가 담긴 데이터, df.td 는 time-dependent covariate 가 담긴 데이터이다. tmerge 함수를 2번 실행하면 두 정보를 합칠 수 있다. 먼저 df.tf 만 이용해서 tstart, tstop 변수를 만들자.

df <- tmerge(df.tf, df.tf, id = id, status1 = event(time, status))

datatable(df, rownames = F, caption = "df: add tstart/tstop", options = list(scrollX = T))

tmerge 2

tmerge 함수의 첫번째는 baseline data, 둘째는 time-dependent covariate 가 담긴 데이터가 들어가지만, tstart, tstop 를 만들기 위해 모두 df.tf 를 넣었다.

status1 이라는 변수를 event(time, status) 로 지정함으로서 tstart, tstop 을 인식할 수 있다.

status1 변수 자체는 status 와 동일하다.

이렇게 만든 df 에 time-dependent 정보가 담긴 df.td 를 결합하면 원하는 데이터를 얻을 수 있다.

tmerge 의 자세한 내용은 추가슬라이드 를 참고하기 바란다.

tmerge 3

df2 <- tmerge(df, df.td, id = id, crp = tdc(time, crp))

datatable(df2, rownames = F, caption = "df2: final", options = list(scrollX = T))

crp 변수를 tdc(time, crp) 로 만들었다. 이제 cox model 을 실행할 수 있는데, 반복측정정보를 cluster 옵션에 넣는 것을 잊지 말자.

tmerge 4

model.td <- coxph(Surv(tstart, tstop, status1) ~ grp + age + crp, data = df2, cluster = id)
summary(model.td)

Call:
coxph(formula = Surv(tstart, tstop, status1) ~ grp + age + crp, 
    data = df2, cluster = id)

  n= 376, number of events= 67 

         coef exp(coef)  se(coef) robust se     z Pr(>|z|)  
grp 0.5022750 1.6524764 0.2525914 0.2555150 1.966   0.0493 *
age 0.0005535 1.0005536 0.0081077 0.0072342 0.077   0.9390  
crp 0.0007922 1.0007925 0.0027391 0.0023373 0.339   0.7347  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

    exp(coef) exp(-coef) lower .95 upper .95
grp     1.652     0.6052    1.0015     2.727
age     1.001     0.9994    0.9865     1.015
crp     1.001     0.9992    0.9962     1.005

Concordance= 0.554  (se = 0.04 )
Likelihood ratio test= 4.21  on 3 df,   p=0.2
Wald test            = 4.34  on 3 df,   p=0.2
Score (logrank) test = 4.18  on 3 df,   p=0.2,   Robust = 4.55  p=0.2

  (Note: the likelihood ratio and score tests assume independence of
     observations within a cluster, the Wald and robust score tests do not).

모수적(parametric) 생존분석

Cox model 은 baseline hazard 없이도 HR을 구할 수 있는 장점이 있다.

다음 식 \[h(t) = h_0(t) \cdot \exp(\sum \beta_i x_i)\] 에서 \(h_0(t)\) 를 몰라도 \(\beta\) 들을 구할 수 있다는 뜻이고, cox model 이 준모수적(semi-parametric) 모형으로 불리는 이유이기도 하다.

그러나 Cox model 로 예측모형을 만들 때 이것은 단점이 된다. \(t\) 년 생존율을 구할 수 없기 때문이다.

생존함수 \(S(t)\) 는 다음처럼 계산하는데 \[S(t) = \int_{0}^{t} h(u) \,du\] baseline hazard 를 모르므로 \(h(t)\) 도 알 수 없고 따라서 \(S(t)\) 도 수식으로 표현할 수 없다.

Cox model 로 예측모형을 만든 연구는 (1) 데이터에서 시간 \(t\) 마다 \(S(t)\) 의 값을 직접 구해 이용하거나, (2) 인구집단통계에서 \(S(t)\) 를 얻어온다.

그러면 baseline hazard 가 어떤 형태라고 가정하면 어떨까? 이것이 모수적 생존분석이며 cox model 과 장단점을 비교하면 다음과 같다.

cox vs parametric

Cox model

– Distribution of survival time unknown

– Less consistent with theoretical \(S(t)\) (typically step function)

+ Does not rely on distributional assumptions

+ Baseline hazard not necessary for estimation of hazard ratio

Parametric Survival Model

+ Completely specified \(h(t)\) and \(S(t)\)

+ More consistent with theoretical \(S(t)\)

+ Time-quantile prediction possible

– Assumption on underlying distribution

weibull

아래는 대표적인 분포들이며 강의에서는 흔히 쓰는 weibull을 다루려 한다.

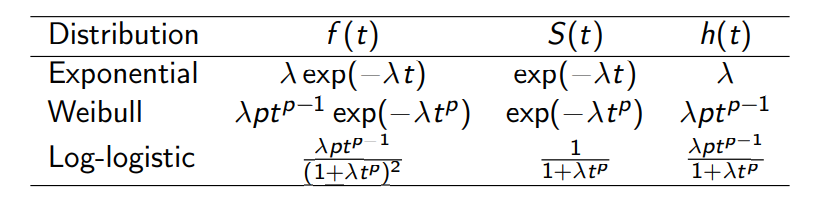
weibull 2

아까 비례위험가정 얘기할 때 weibull 모형은 log-log 그래프가 직선인지도 확인해야 한다고 했는데, 그 이유는 아래 식에 나와있듯이 \(\log(-\log(S(t)))\) 와 \(\log(t)\) 가 정비례관계이기 때문이다.

\[ \begin{align} S(t) &= \exp(-\lambda t^p) \\ -\log(S(t)) &= \lambda t^p \\ \log(-\log(S(t))) &= \log(\lambda) + p\log(t) \\ \log(-\log(S(t))) &\propto \log(t) \end{align} \]

\(p\) 를 scale parameter 라 하며 \(p = 1\) 이면 baseline hazard 가 시간에 따라 일정함을 의미하며, 자세한 내용은 parametric survival models lecture note 를 참고하자.

weibull 3

R의 survreg 함수를 이용하며, 결과해석은 cox model 과 동일한데 scale parameter 값이 추가로 나온다 (scale parameter를 미리 정할 수도 있다).

model.weibull <- survreg(Surv(time, status) ~ trt, data = veteran)
summary(model.weibull)

Call:
survreg(formula = Surv(time, status) ~ trt, data = veteran)
             Value Std. Error     z      p
(Intercept) 4.7218     0.3275 14.42 <2e-16
trt         0.0478     0.2079  0.23  0.818
Log(scale)  0.1585     0.0673  2.35  0.019

Scale= 1.17 

Weibull distribution
Loglik(model)= -748.1   Loglik(intercept only)= -748.1
    Chisq= 0.05 on 1 degrees of freedom, p= 0.82 
Number of Newton-Raphson Iterations: 5 
n= 137 

weibull 4

Scale = 1.17 임을 확인할 수 있고, trt 그룹별 \(S(t)\) 를 그려보면 아래와 같다.

pcut <- seq(0.01, 1, by = 0.01)  ## 1%-99%
ptime <- predict(model.weibull, newdata = data.frame(trt = 1), type = "quantile", p = pcut, se = T)
matplot(cbind(ptime$fit, ptime$fit + 1.96*ptime$se.fit, ptime$fit - 1.96*ptime$se.fit), 1 - pcut,
        xlab = "Days", ylab = "Survival", type = 'l', lty = c(1, 2, 2), col=1)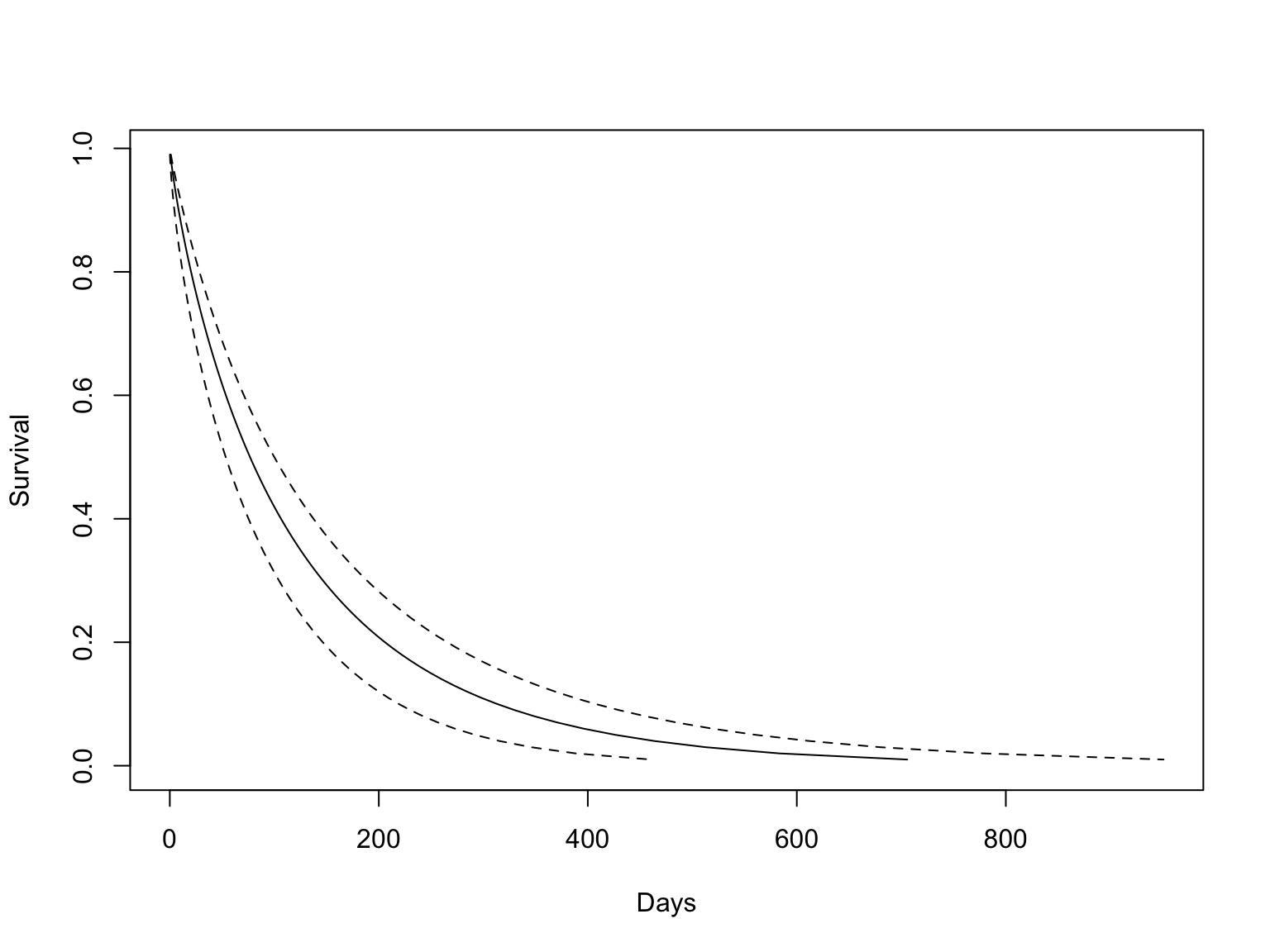

weibull vs cox

\(S(t)\) 를 구할 수 없는 cox model 의 그림과 비교해보자.

model.cox <- exp
kmfit.exp <- survfit(exp, newdata = data.frame(trt = 1))
plot(kmfit.exp, lty = c(1, 2, 2), col=1, lwd=2, xlab = "Days", ylab = "Survival")

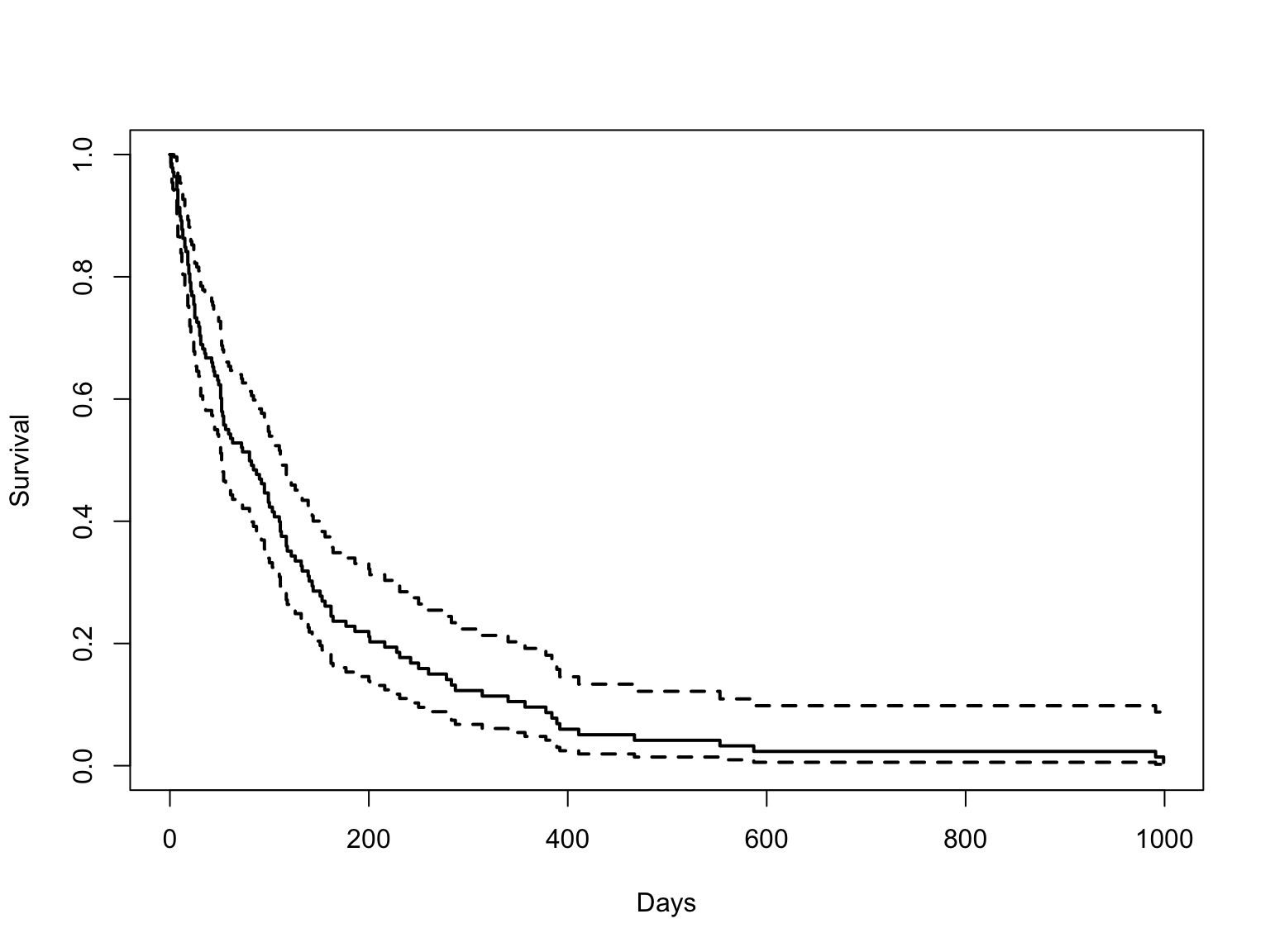
Summary

지금까지 생존분석 때 고려할 내용을 다루었으며 처음의 요약을 반복하면 아래와 같다.

• 자체 개발한 jskm 패키지로 kaplan-meier 그림을 그린다.

• Log-log plot, Observed-expected plot 으로 비례위험가정을 확인 후, cox.zph 함수로 p-value 를 구한다.

• anova 로 여러 모형의 log-likelihood 를 비교하고, step 으로 AIC 기반 최적모형을 고를 수 있다.

• Time-dependent analysis 는 (1) 비례위험가정이 깨졌을 때, (2) 반복측정 공변량이 있을 때 수행한다.

• 모수적 생존분석은 생존함수 \(S(t)\) 를 구할 수 있어 예측모형을 만들 수 있다.