정규분포(Normal Distribution)

김진섭

HEADLINE

정규분포의 위대함

by 이항분포

by 오차의 법칙

by 중심극한정리

시행 횟수/표본 개수 \(n\)이 커질수록 표본평균 \(\bar{X}\)는 \(N(\mu,\frac{\sigma^2}{n})\)을 따른다.

Intro
이항분포의 근사
오차의 법칙: 오차라면 마땅히 가지고 있어야 할 조건
중심극한정리: 모양이 일그러진 동전 / 주사위 던지기
중심극한정리: 표준정규분포 / 카이제곱분포
중심극한정리 고찰
Conclusion

목표

정규분포(Normal distribution)의 위대함과 당위성 이해
연속변수는 대부분 정규분포를 가정
실제로 키, 몸무게, 시험 점수 등 대다수의 측정값은 정규분포
Why?
이항분포의 근사, 오차의 법칙, 중심극한정리

이항분포(Binomial Distribution)

이항분포 \(B(n,p)\) : 확률 \(p\)인 사건을 \(n\)번 시행 시 각 사건들 확률분포
평균: \(np\), 분산: \(np(1-p)\)
이항분포가 삶의 대부분(선거, 타율, 객관식시험..)
정규분포가 이항분포의 근사값으로 표현된다면?

이항분포 근사: 동전을 무한히 던지면?

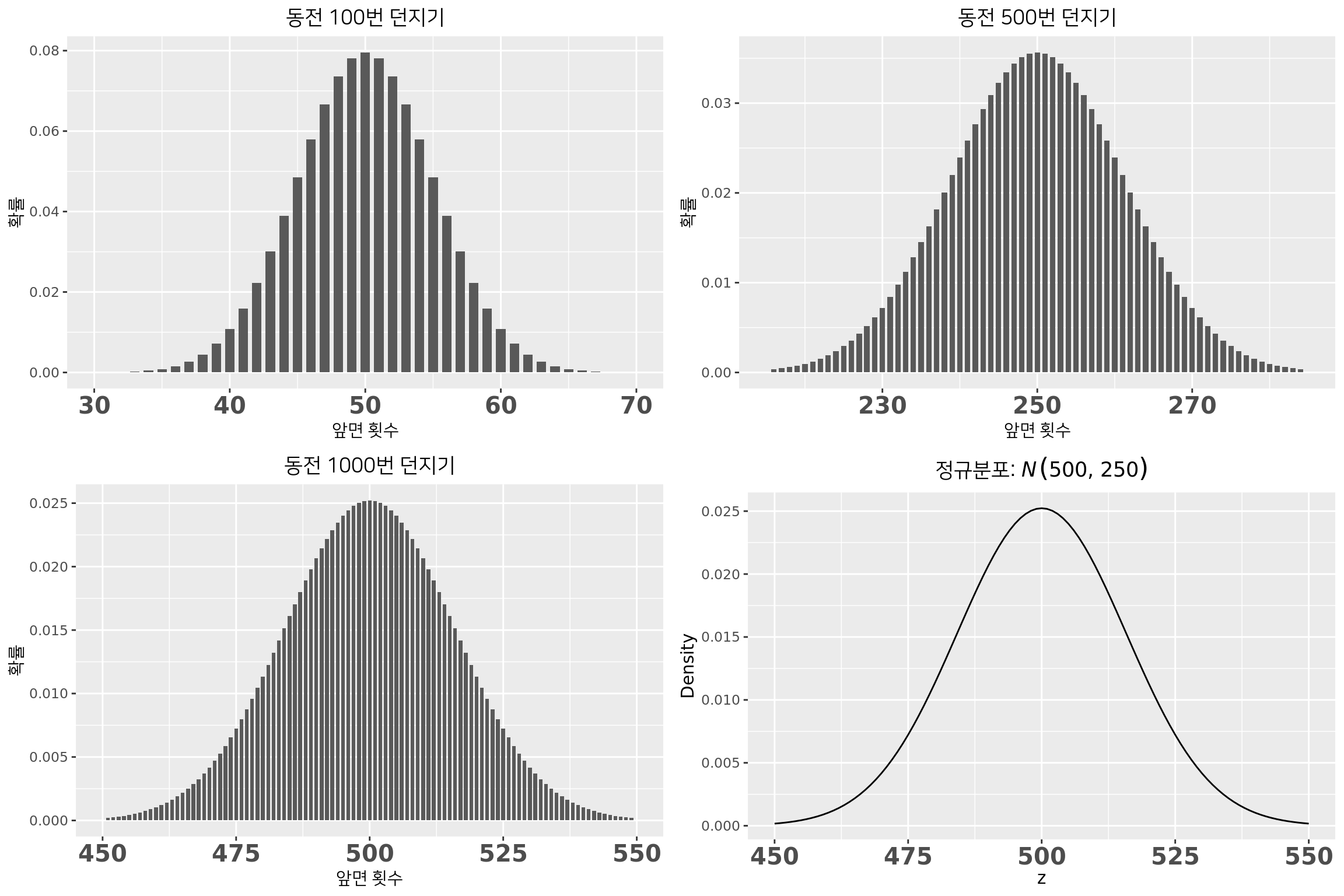
이항분포 VS 정규분포: 동전 던지기

\(B(1000,\frac{1}{2}) \simeq N(1000\times \frac{1}{2}, 1000\times \frac{1}{2} \times \frac{1}{2})\)

이항분포의 근사: 주사위를 무한히 던지면?

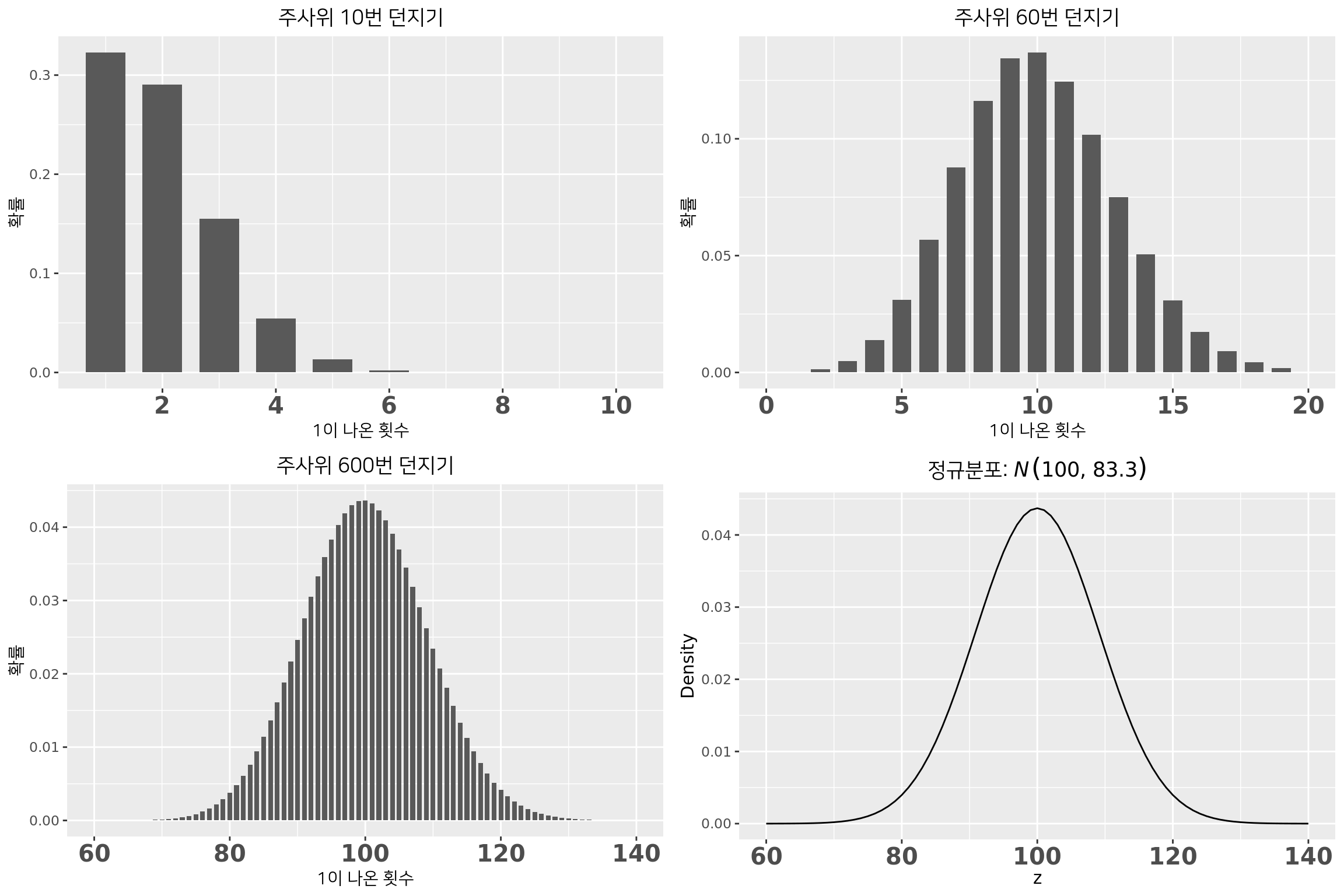
이항분포 VS 정규분포: 주사위 던지기

\(B(600,\frac{1}{6}) \simeq N(600\times \frac{1}{6}, 600\times \frac{1}{6} \times \frac{5}{6})\)

이항분포 근사: 일반화

동전과 주사위 예시
- \(B(1000,\frac{1}{2}) \simeq N(1000\times \frac{1}{2}, 1000\times \frac{1}{2} \times \frac{1}{2})\)
- \(B(600,\frac{1}{6}) \simeq N(600\times \frac{1}{6}, 600\times \frac{1}{6} \times \frac{5}{6})\)
일반화, \(n\)이 커질수록
- \(B(n,\frac{1}{2}) \simeq N(n \times \frac{1}{2}, n \times \frac{1}{2} \times \frac{1}{2})\)
- \(B(n,\frac{1}{6}) \simeq N(n \times \frac{1}{6}, n \times \frac{1}{6} \times \frac{5}{6})\)
종합
- 시행횟수 \(n\)이 커질수록 \(B(n,p) \simeq N(np, np(1-p))\)
- 정규분포가 이항분포의 근사로 설명, 이상분포의 지위를 물려받는다.

오차의 법칙: 오차라면 마땅히 이래야

수학자 Gauss는 오차에 대한 고찰만으로 정규분포를 유도.

1. +오차와 -오차가 나올 가능성 같다: \(f(-\epsilon)=f(\epsilon)\)인 좌우대칭 함수
1. 작은 오차가 흔하고 큰 오차는 드물다: \(f(\epsilon)\)는 위로 볼록한 모양
1. \(f(\epsilon)\)는 부드러운 모양(2번 미분가능)이고 확률의 합은 1: \(\int_{-\infty}^{\infty} f(\epsilon) d\epsilon=1\)
4. 오차의 참값일 가능성이 가장 높은(MLE) 값은 측정한 오차들의 평균

-> 측정값이 각각 \(\epsilon_1, \epsilon_2, \cdots, \epsilon_n\)일 때 가능도 \(L=f(\epsilon_1 - \epsilon)f(\epsilon_2 - \epsilon)\dots f(\epsilon_n - \epsilon)\)는 \(\epsilon=\frac{\epsilon_1+\epsilon_2+\cdots+\epsilon_n}{n}\)에서 최대

정말 간단한 4개 조건만으로 정규분포 PDF를 수학적으로 유도.

정규분포가 대부분일 것이다

중심극한정리: 무조건 정규분포 OK?

평균은 가장 흔히 쓰이는 지표.
표본을 뽑아 표본평균(Sample mean) 구하여 전체 평균으로 간주
믿음의 정도로 표준오차(Standard error, 표본평균들의 표준편차) 이용
수백, 수천 명의 여론조사를 민심의 척도로 간주해도 되나?

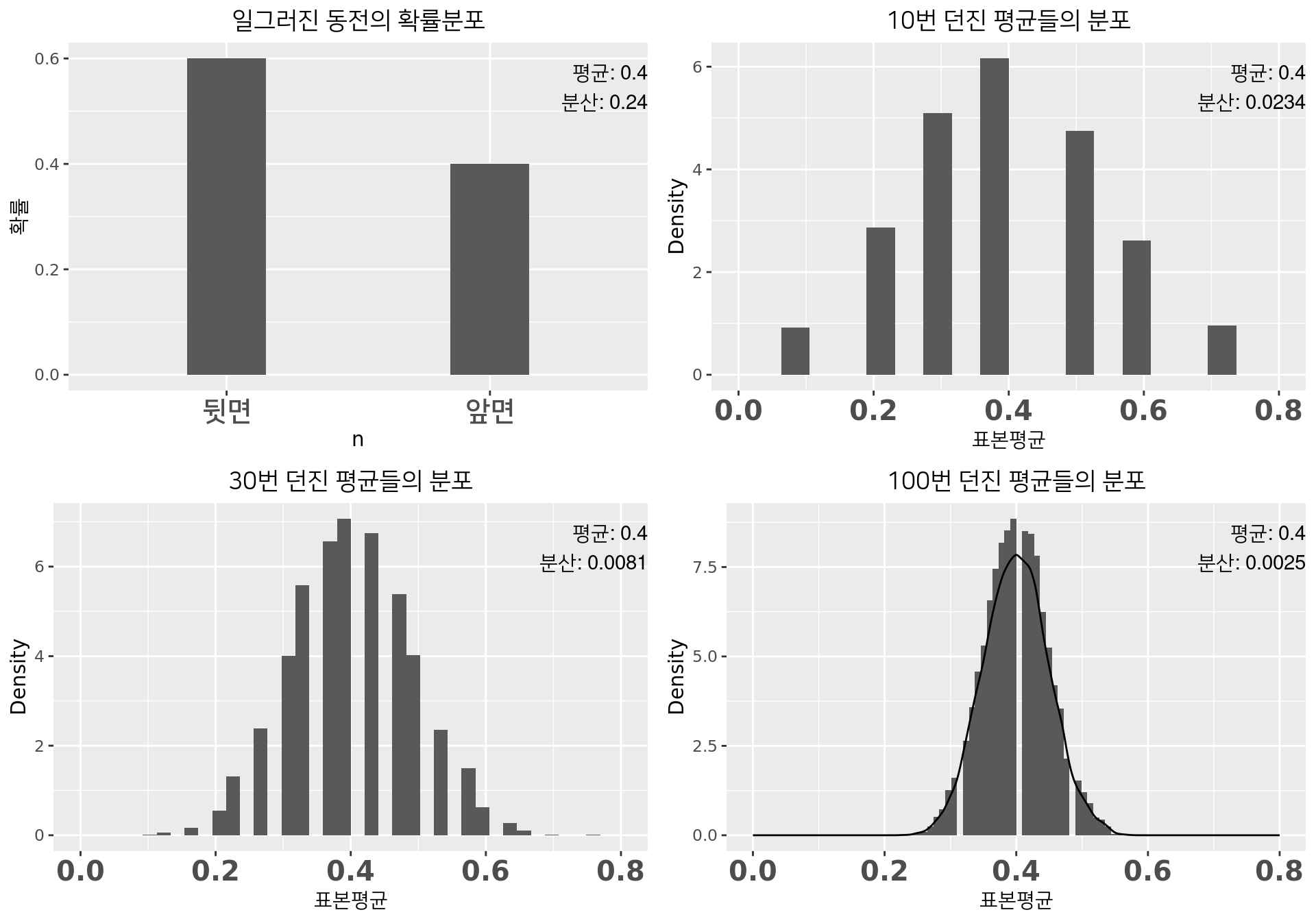
예: 일그러진 동전 \(p = 0.4\)

행위 1: 10번 던져 앞면 나올 확률 \(\hat{p}\) 계산
행위 1 을 10000번 수행하여 \(\hat{p}\) 의 분포 확인, 행위 2은 30번, 행위 3은 100번 던지기

\(n\) 커질수록 \(\hat{p}\) 이 정규분포에 가까워짐
\(\hat{p}\)의 평균이 실제 \(p\)값인 0.4에 가까워짐
\(\hat{p}\)의 분산이 \(\frac{0.24}{n}=\frac{p(1-p)}{n}\)에 가까워짐

따라서 \(n\)이 커지면 \(\hat{p}\) 는 \(N(p,\frac{p(1-p)}{n})\) 을 따른다

주사위 던지기

주사위눈 평균(\(\mu\)): \(\frac{1+2+3+4+5+6}{6}=3.5\), 분산(\(\sigma^2\)): \(\frac{(1-3.5)^2+(2-3.5)^2+\cdots+(6-3.5)^2}{6}\approx 2.92\)
행위 1: 10번 던져 평균 \(\bar{x}\) 구하는 작업을 10000번 반복. 행위2, 3은 앞과 동일

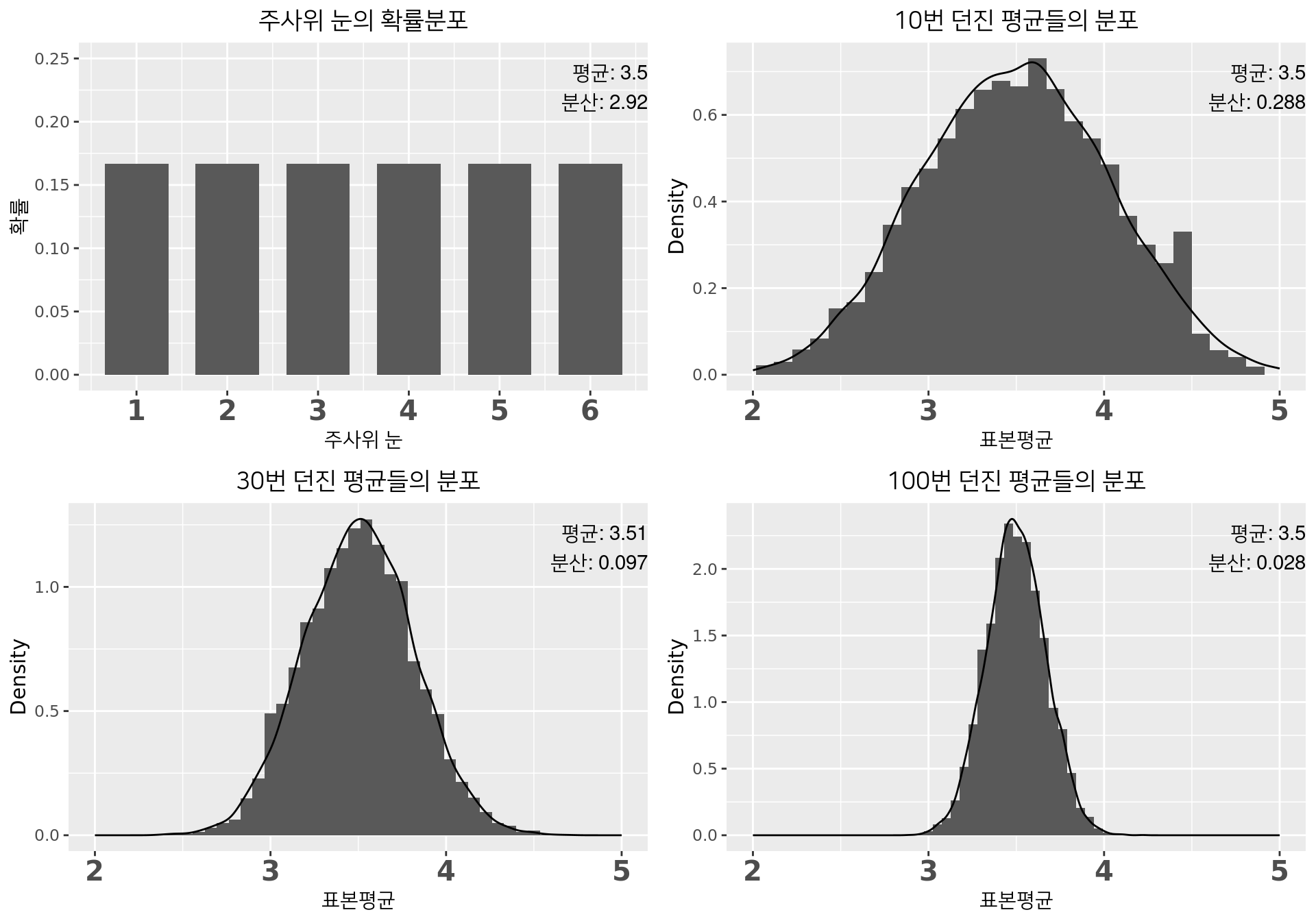
\(n\)이 커지면 표본평균 \(\bar{X}\)의 분포 \(\simeq\) 정규분포
\(\bar{X}\)의 평균 \(\simeq\) 실제 평균인 \(\mu=3.5\)
\(\bar{X}\)의 분산 \(\simeq\) \(\frac{2.92}{n}=\frac{\sigma^2}{n}\)

\(n\)이 커지면 \(\bar{X}\)는 \(N(\mu,\frac{\sigma^2}{n})\)을 따른다.

표준정규분포

표준 정규분포(\(\mu=0\), \(\sigma^2=1\))에서 \(n\)개 뽑아 평균내기
세팅은 이전과 동일

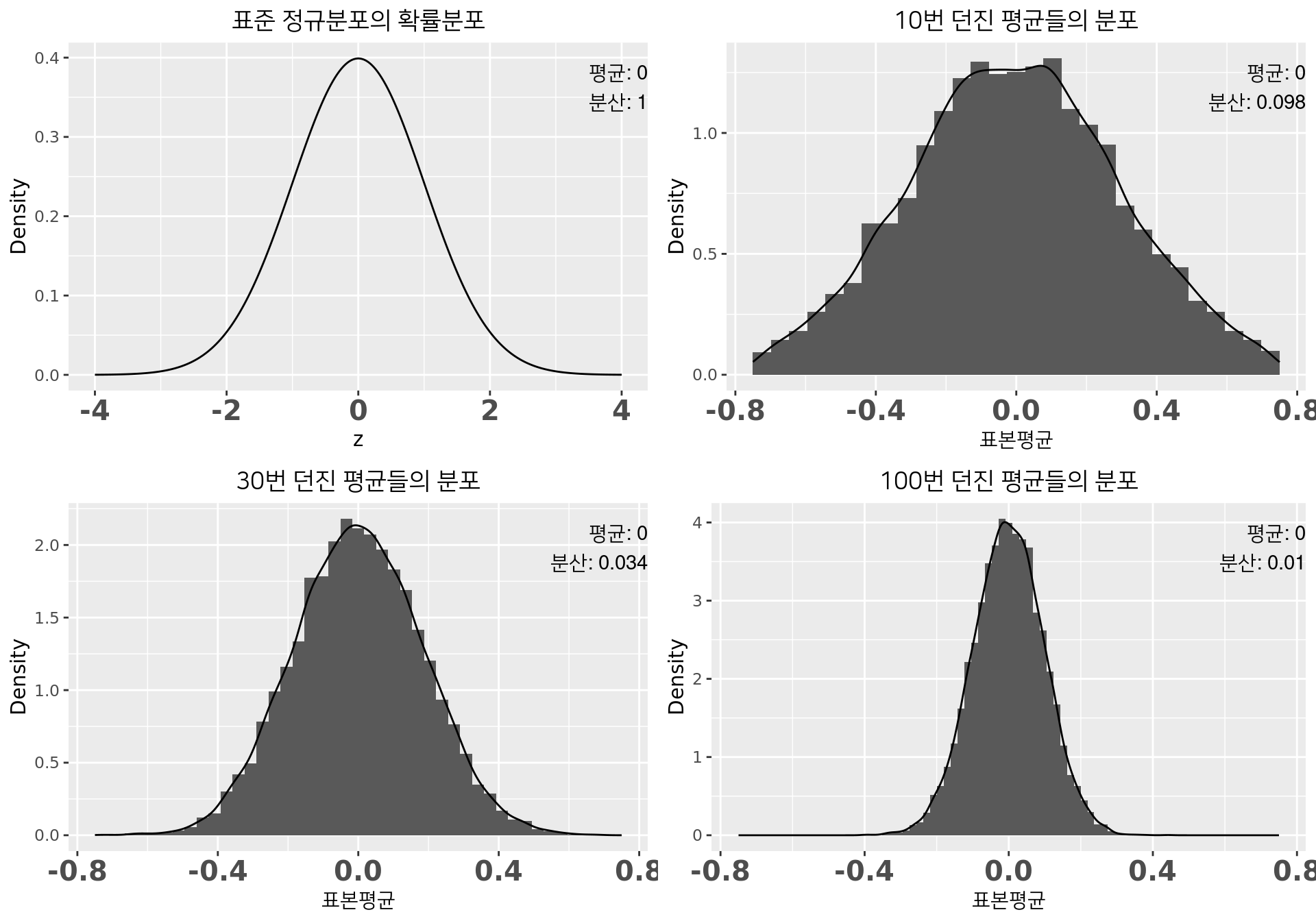
\(n\)이 커질수록 표본평균 \(\bar{X}\) 분포 \(\simeq\) 정규분포
\(\bar{X}\)의 평균 \(\simeq\) 실제평균 0
\(\bar{X}\)의 분산 \(\simeq\) \(\frac{1}{n}\)에 가까워졌다.

연속확률의 경우에도 \(n\)이 커지면 \(\bar{X}\)는 \(N(\mu,\frac{\sigma^2}{n})\)을 따른다.

카이제곱분포

자유도 1인 카이제곱분포(\(\mu=1\), \(\sigma^2=2\)): 왼쪽으로 치우친 분포에서 뽑아도?
세팅은 동일

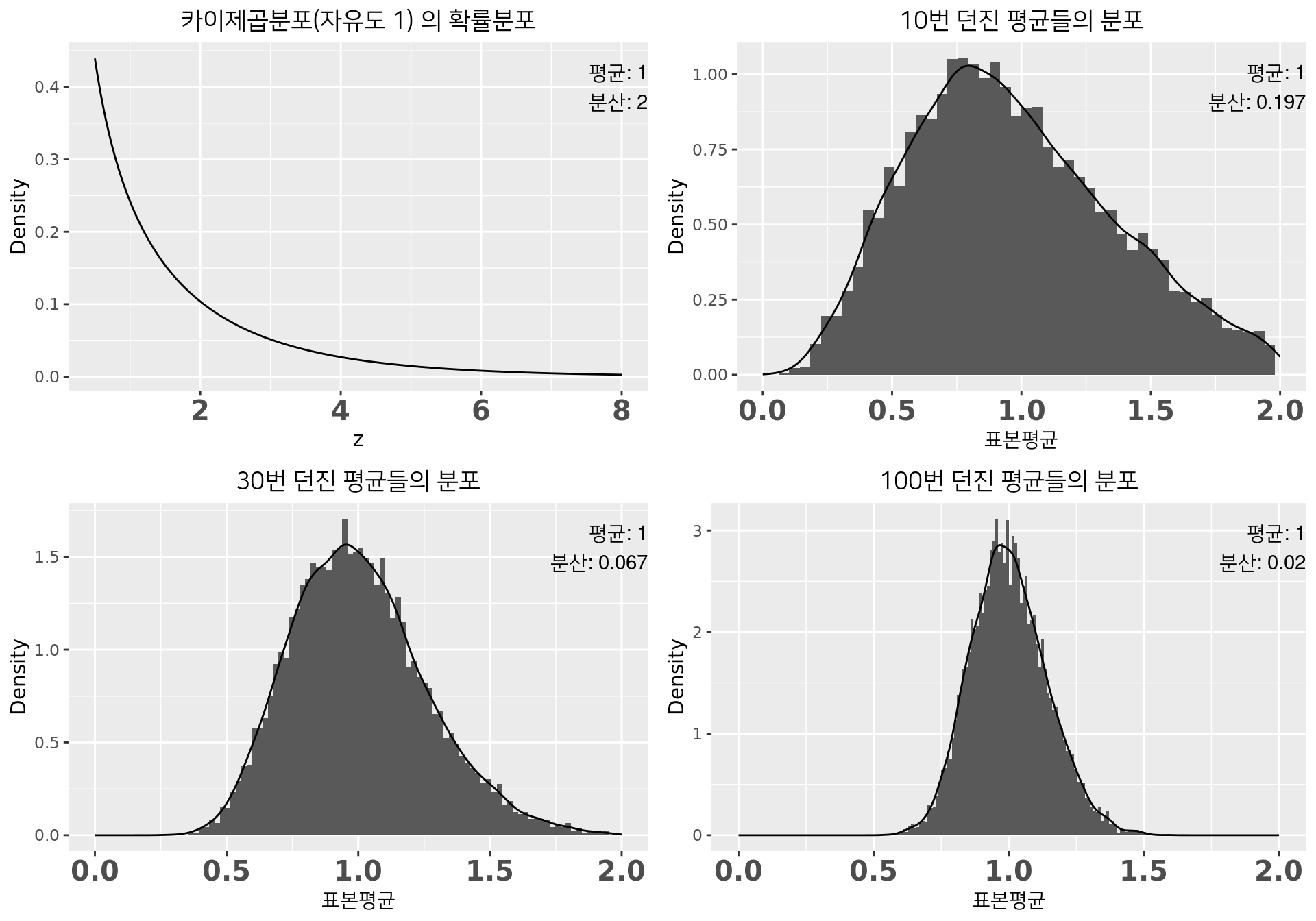
\(n\)이 커질수록 \(\bar{X}\)의 분포 \(\simeq\) 정규분포
\(\bar{X}\)의 평균과 분산이 각각 1, \(\frac{2}{n}\)에 가까워짐

\(\bar{X}\)는 \(n\)이 커질수록 \(N(\mu,\frac{\sigma^2}{n})\)을 따른다.

중심극한정리

중심극한정리(Central Limit Theorem, CLT) : 어떤 모집단이든 30개 정도의 \(\bar{X}\)가 확보되면 정규분포를 따른다.

중심극한정리 고찰 - 쪽수가 깡패(?)

\(n\) 이 커질수록

표본평균의 평균이 모집단 평균에 가까워짐
표준오차(표본평균의 분산) \(\frac{\sigma^2}{n}\) 이 0에 가까워짐

즉, 표본평균을 실제평균으로 간주해도 됨

중심극한정리 고찰 - 의심의 정도를 숫자로 표현(p-value)

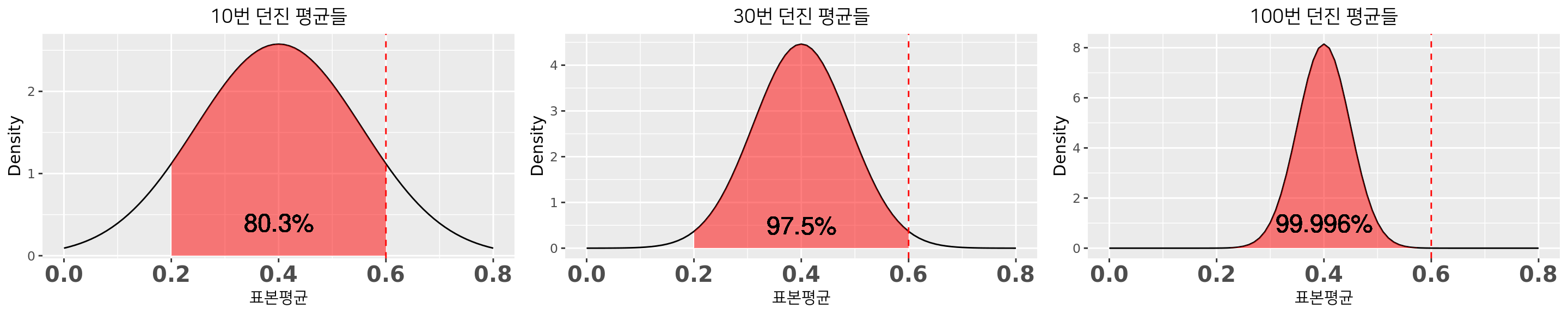
예: \(p = 0.4\) 인 일그러진 동전 여러번 던지기

여러번 던져서 계산한 \(\hat{p}\)의 분포가 \(N(0.4,0.024)\)에 가까워짐.
10번 던져서 앞면 6번(\(\hat{p}=0.6\)) 나왔다면? 6번 이상 나올 확률: 19.7% \(\div2\) = 9.85% -> 그럴 수 있지
30번 던져서 앞면 18번(\(\hat{p}=0.6\)) 나왔다면? 18번 이상 나올 확률: 2.5% \(\div2\) = 1.25% -> 이상한데
100번 던져서 앞면 60번(\(\hat{p}=0.6\)) 나왔다면? 60번 이상 나올 확률: 0.004% \(\div2\) = 0.002% -> 동전조작!

Conclusion

정규분포의 위대함을 설명하는 3개의 논리, 중심극한정리 고찰