가능도(Likelihood)
vs 확률(Probability)
HEADLINE
기억해 두자.
셀 수 있는 사건 : 확률 = 가능도
셀 수 없는 사건 中 특정 사건이 일어날 확률 = 0
셀 수 없는 사건 : PDF값 = 가능도
진실을 찾는 방법 : 최대가능도 추정량(Maximum Likelihood Estimator, MLE)
Contents
Intro
이산사건의 확률
연속사건의 확률
가능도(Likelihood) : 연속사건 中 특정 사건이 일어날 가능성
사건이 여러번 일어날 경우의 가능도
최대가능도 추정량(Maximum Likelihood Estimator, MLE) : 모양이 일그러진 동전
최대가능도 추정량(Maximum Likelihood Estimator, MLE) : 나의 실제 키
Conclusion
Intro
- 가능도(Likelihood) 의 직관적 이해가 목표
- 중요한 개념 but 의학통계 책에서는 생략.
- 확률(Probability)과의 비교
- 최대가능도 추정량(Maximum Likelihood Estimator) 이해
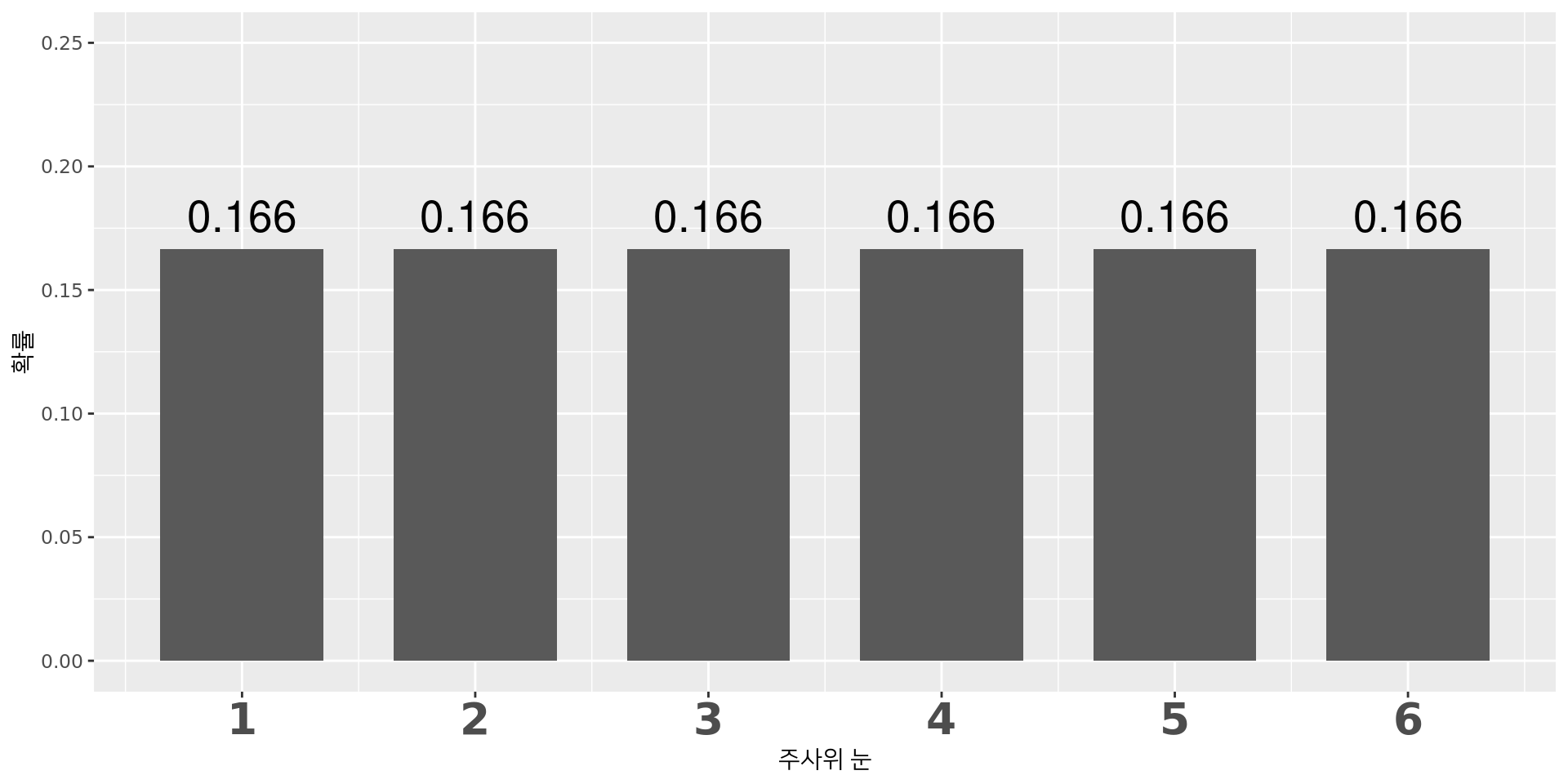
이산사건의 확률: 주사위
- 가능한 숫자는 1,2,3,4,5,6
- 각 숫자가 나올 확률은 \(\frac{1}{6}\) 동일.
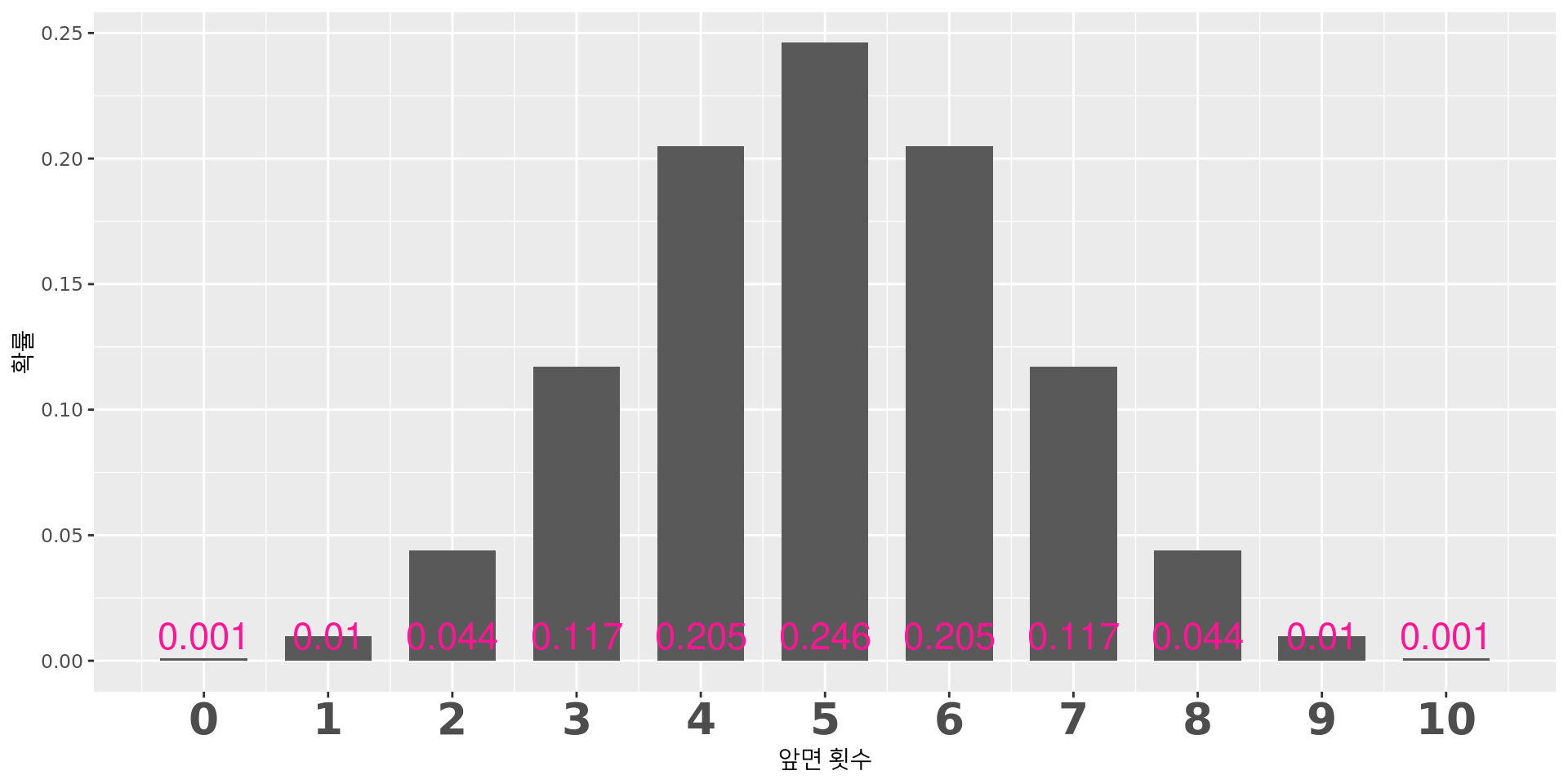
이산사건의 확률: 동전
- 10번 던질 때 앞면나오는 횟수 \(n\)
- 확률은 \(p = _{10}C_{n}\frac{1}{2}^n\frac{1}{2}^{10-n} = _{10}C_{n}\frac{1}{2}^{10}=\frac{_{10}C_{n}}{1024}\)
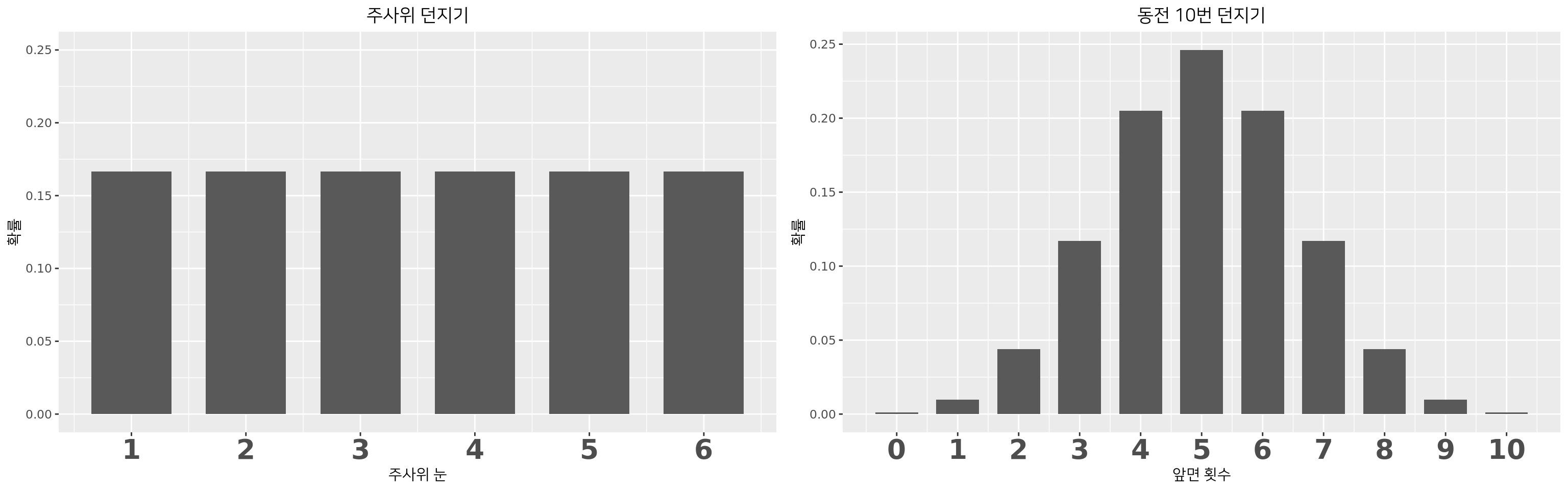
이산사건의 확률 = 가능도
- 총 사건의 갯수를 셀 수 있음(ex: 6, 11개).
- 따라서 각 확률을 계산가능(합=1).
- 확률 = 가능도 로 정의.
연속사건의 확률: 랜덤 숫자(실수) 뽑기
- 1 ~ 6의 실수 랜덤으로 뽑기
- 1 ~ 6 사이 무한히 많은 실수 존재
- 5가 뽑힐 확률 = \(\frac{1}{\infty}=0\)
- 4가 뽑힐 확률도 마찬가지, 즉 특정 사건의 확률은 모두 0.
- 끝?
연속사건의 확률: 특정구간의 확률
- 5가 뽑힐 확률은 0 but, 4 ~ 5 가 뽑힐 확률은 \(\frac{5-4}{6-1}=0.2\).
- 연속사건은 특정 구간에 속할 확률 이용: 확률밀도함수(Probability Density Function: PDF)
- PDF 그래프에서 특정 구간에 속한 넓이 = 특정 구간에 속할 확률, 전체 넓이는 1
PDF 예시: 실수 뽑기
- PDF: 1 ~ 6 은 모두 0.2, 나머지는 0.
- 2 ~ 4 가 뽑힐 확률은 \(2\times 0.2 = 0.4\).
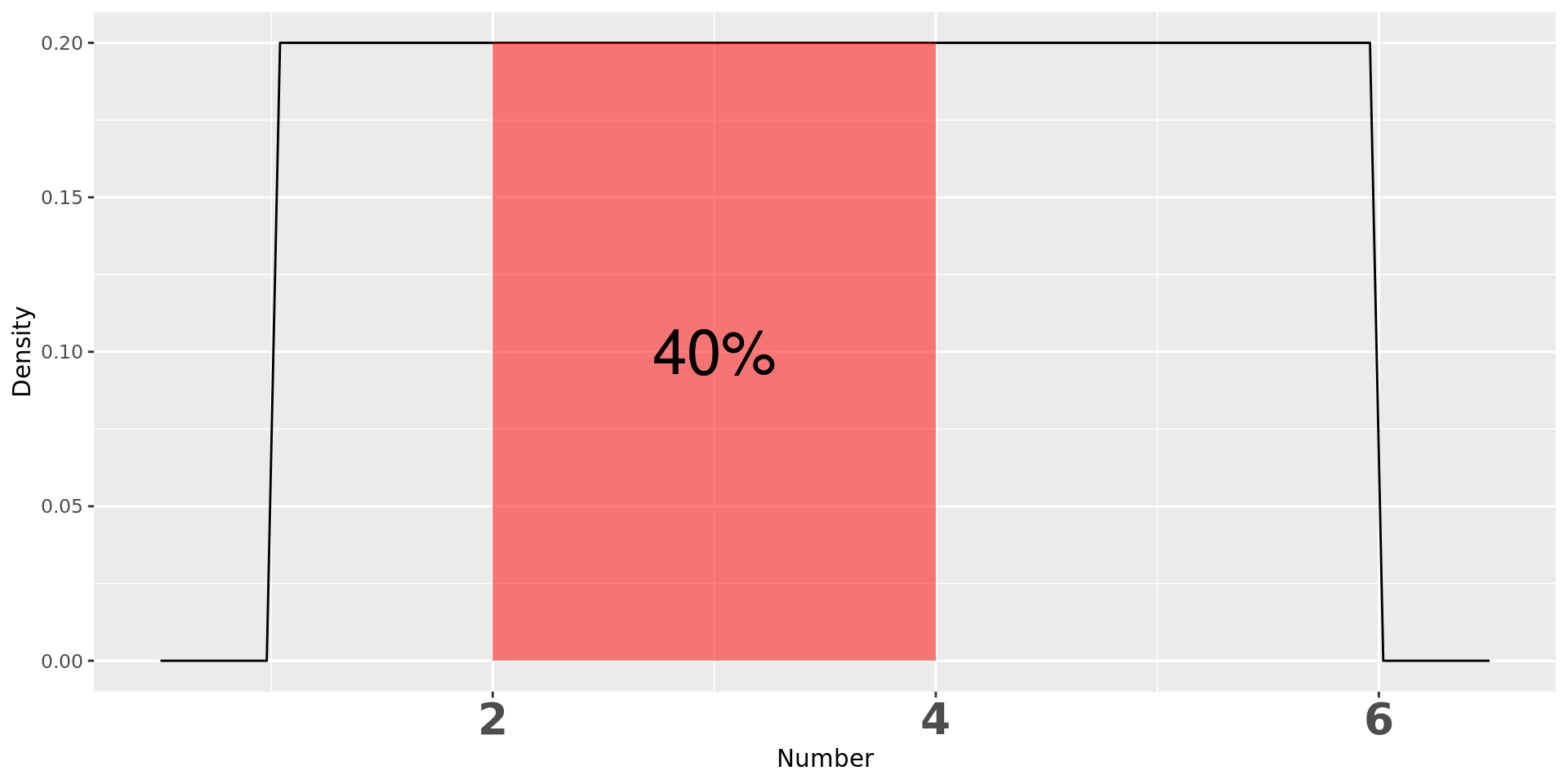
1 ~ 6의 숫자 뽑기
PDF 예시: 표준정규분포
- 평균 0, 분산 1 인 정규분포
- PDF는 \(\frac{1}{\sqrt{2\pi}}e^{-z^2/2}\)
- \(z\)가 특정 값일 확률은 전부 0
- -1.96 ~ 1.96 일 확률은 0.95: p-value
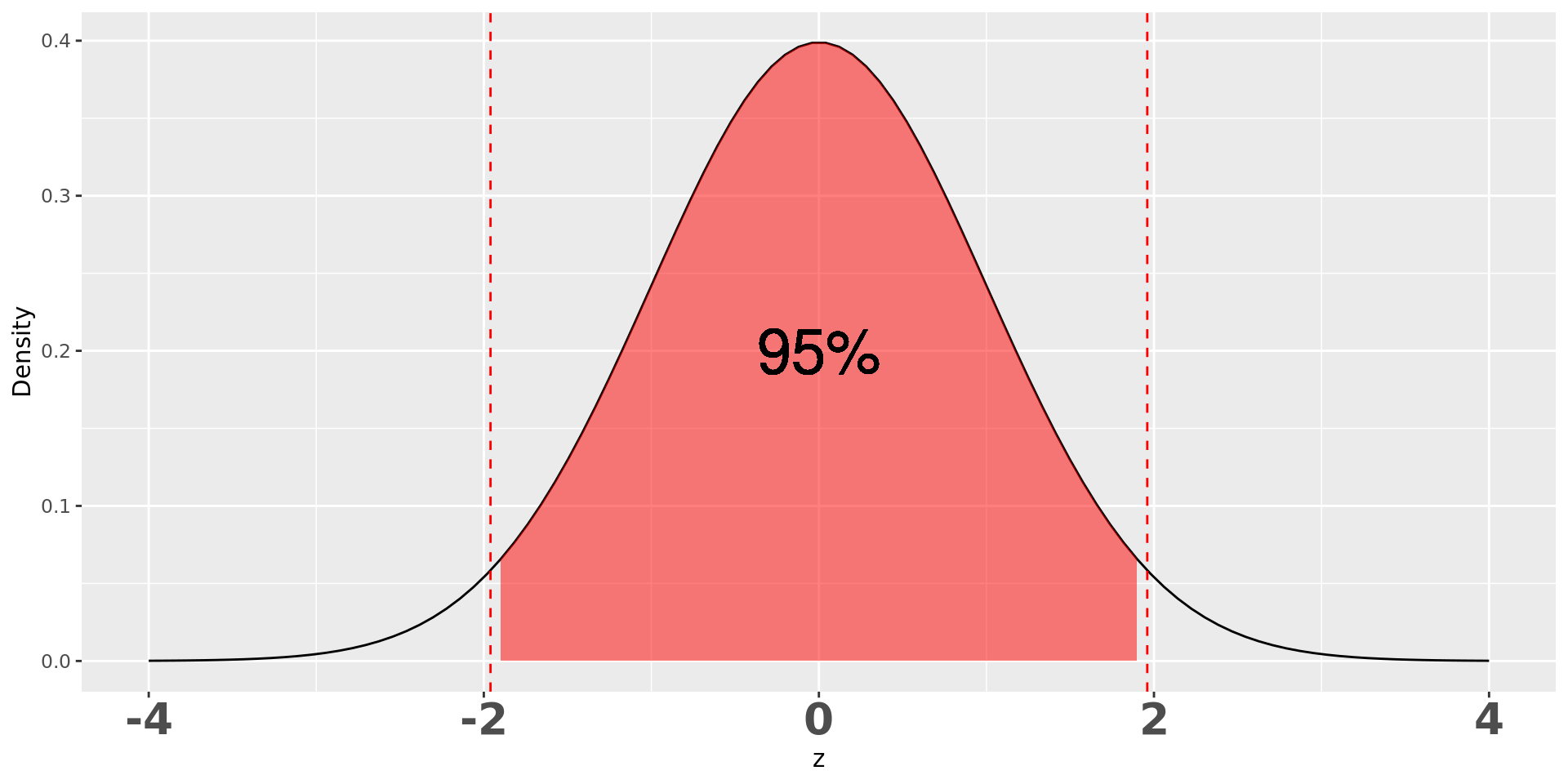
표준정규분포 PDF
표준정규분포: 특정사건 비교는 포기?
- \(z\) 가 -2, 0, … 999 등 특정 숫자일 확률은 모두 0
- 따라서 각 사건의 발생가능성 차이는 없다? But
- 가장 솟아 있는 0 근처가 가능성 높고, 0에서 멀어질수록 가능성이 낮음을 느끼고있다.
- 확률 은 연속사건의 가능성 차이를 나타낼 수 없음
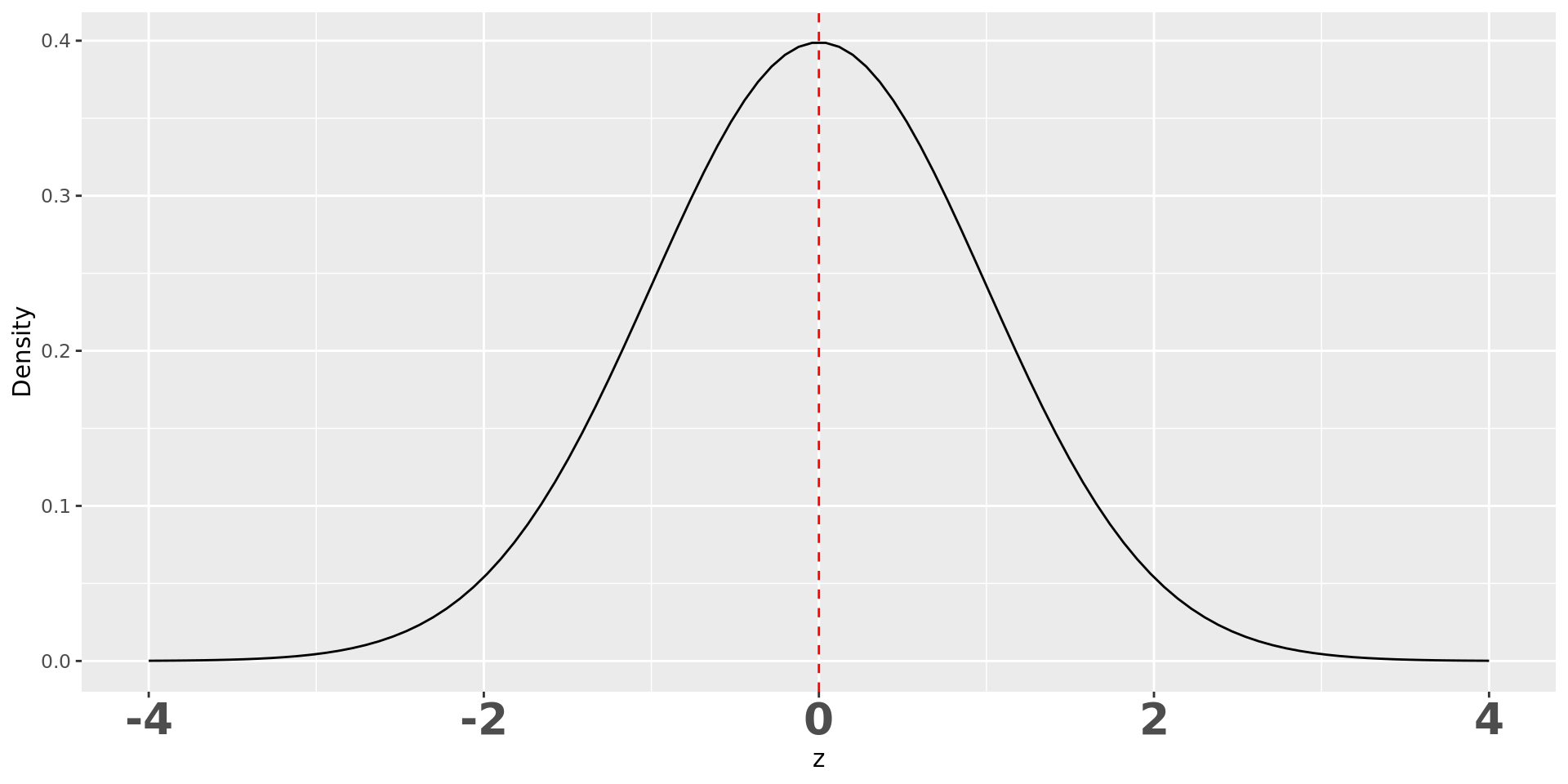
표준정규분포의 PDF
가능도 in 연속사건: 특정 사건의 가능성
PDF값을 가능도로 정의.
- 가능도의 직관적인 정의 : 확률밀도함수의 \(y\)값 (PDF)
- 이산사건: 확률 = 가능도
- 연속사건: 확률 \(\neq\) 가능도 => PDF값 = 가능도

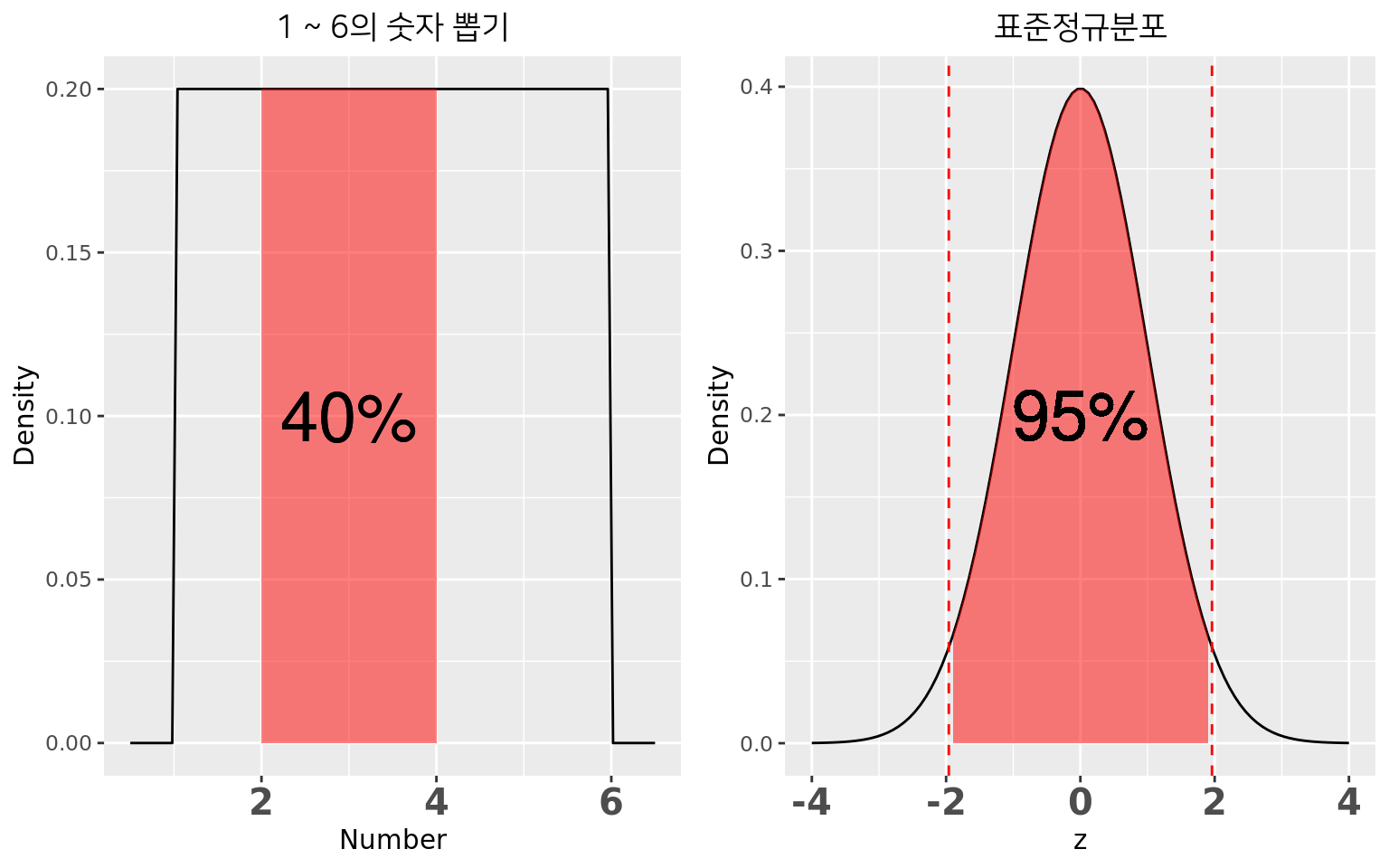
가능도 응용: 사건이 여러번 일어난다면?
주사위 3번 던져 1,3,6이 나올 확률 = \(\frac{1}{6}\times\frac{1}{6}\times\frac{1}{6}=\frac{1}{216}\)
동전 10번 던져서 앞면 갯수 세기 를 3회 시행하여 앞면이 2,5,7번 나올 확률
=> 0.044 \(\times\) 0.246 \(\times\) 0.117\(=\) 0.001
이산사건 확률 = 가능도 이므로 각 예시의 가능도도 \(\frac{1}{216}\)과 0.001
가능도 응용: 연속사건이 여러번?
표준정규분포에서 3번 뽑을때 -1, 0, 1이 나올 확률과 가능도는?
확률 : 각 사건이 일어날 확률은 모두 0이므로 0
가능도 : 각 사건의 가능도가 0.24, 0.4, 0.24이므로 0.24 \(\times\) 0.4 \(\times\) 0.24 \(=\) 0.02
연속사건에서 가능도와 확률은 다르다
최대가능도 추정량(Maximum Likelihood Estimator, MLE)
이산사건: 모양이 일그러진 동전
- 앞면확률 \(p \neq 0.5\), 알려면 실제 던져봐야..
- 1000번 던져 앞면 400번 나왔다면 \(p=0.4\)?
- 이 사건이 일어날 가능성 \(L=_{1000} C_{400}p^{400}(1-p)^{600}\)
- 가능성 \(L\)을 최대(MLE)로 만드는 \(p=0.4\)
- 일그러진 동전의 앞면나올 확률은 0.4라고 추정. 직관과 일치
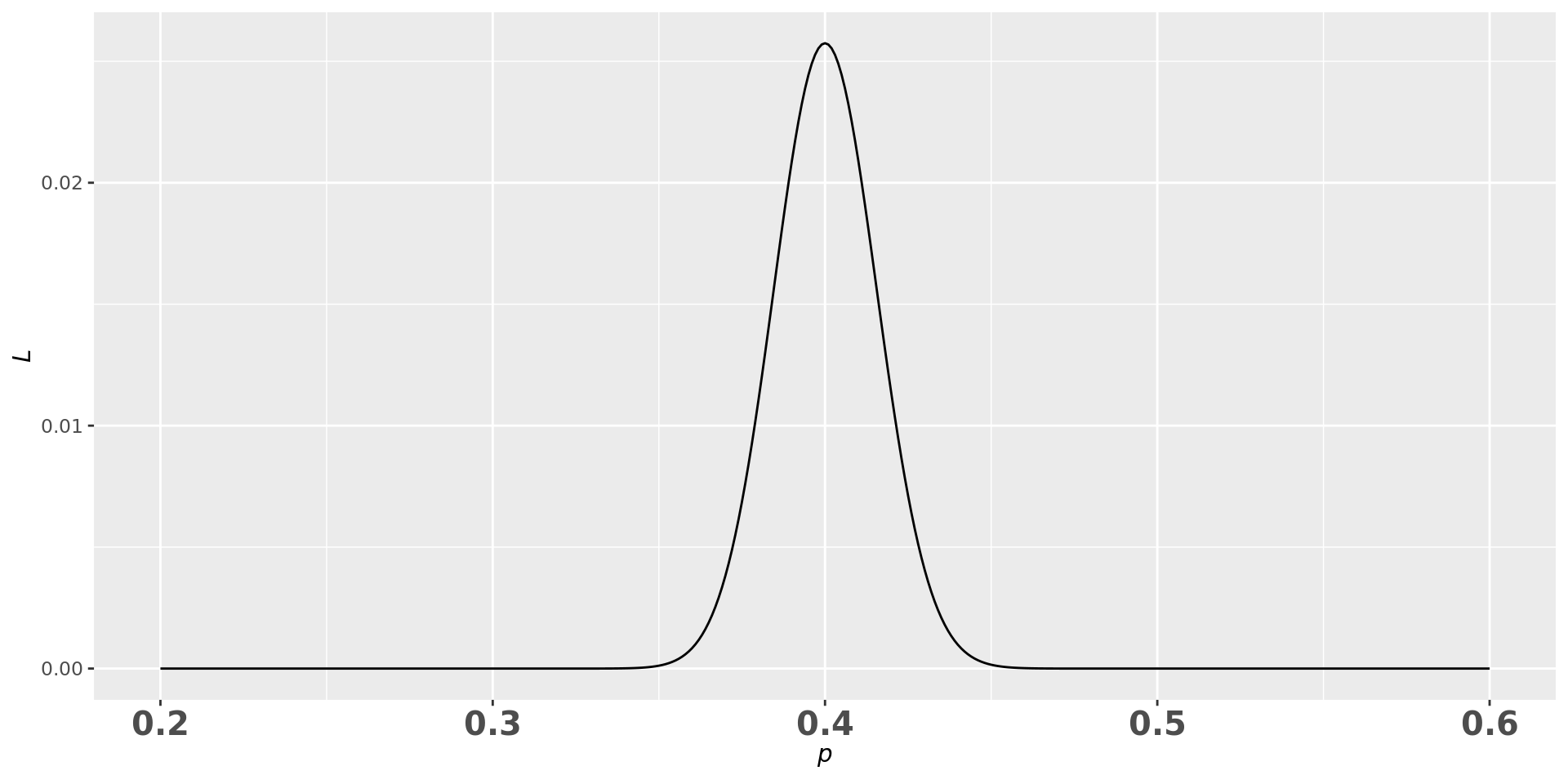
동전 앞면이 나올 확률 \(p\)에 따른 가능도 \(L\)
연속사건: 키
5번 측정결과 178, 179, 180, 181, 182(cm) 일때 실제 키는 평균값?
가정: 키측정은 정규분포를 따른다(평균 \(\mu\), 분산 \(\sigma^2\))
측정값 \(x\)에 해당하는 가능도 = \(\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)
위 5번 측정결과가 나타날 가능성 \(L\) \(=\frac{1}{\sqrt{2\pi}\sigma^2}e^{-\frac{(178-\mu)^2}{2\sigma^2}}\times\frac{1}{\sqrt{2\pi}\sigma^2}e^{-\frac{(179-\mu)^2}{2\sigma^2}}\times\frac{1}{\sqrt{2\pi}\sigma^2}e^{-\frac{(180-\mu)^2}{2\sigma^2}}\times\frac{1}{\sqrt{2\pi}\sigma^2}e^{-\frac{(181-\mu)^2}{2\sigma^2}}\times\frac{1}{\sqrt{2\pi}\sigma^2}e^{-\frac{(182-\mu)^2}{2\sigma^2}}\)
\(L\)이 최대이려면 \((178-\mu)^2+(179-\mu)^2+(180-\mu)^2+(181-\mu)^2+(182-\mu)^2\)이 최소여야 함. \(\mu=180\)일 때 최소.
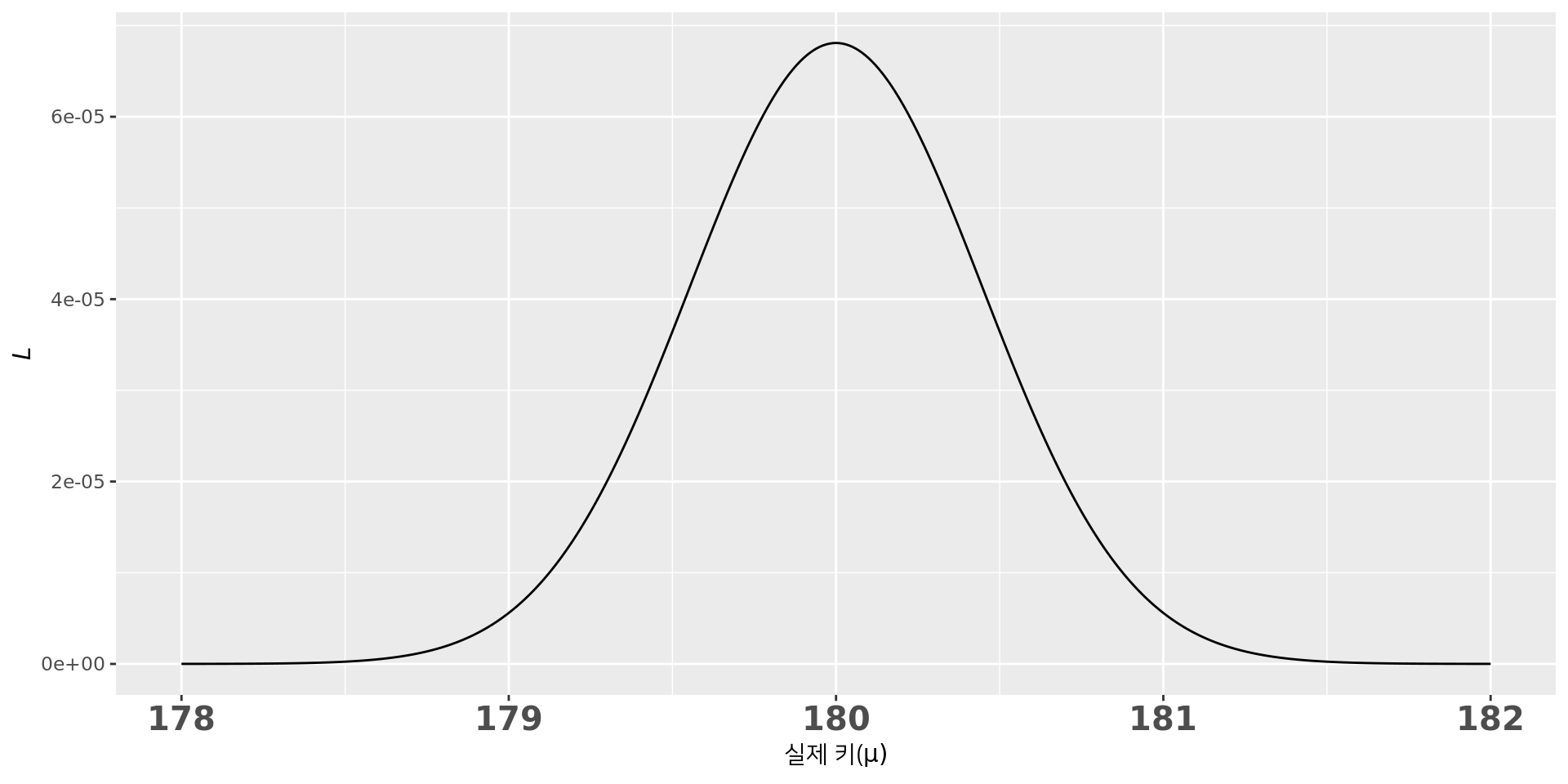
실제 키에 따른 가능도 \(L\)
Conclusion
셀 수 있는 사건 : 확률 = 가능도
셀 수 없는 사건 中 특정 사건이 일어날 확률 = 0
셀 수 없는 사건 : PDF값 = 가능도
진실을 찾는 방법 : 최대가능도 추정량(Maximum Likelihood Estimator, MLE)

www.zarathu.com