Generalized Additive Model(GAM)

Zarathu Co.,Ltd

Jinseob Kim

Executive summary

GAM 은 비선형관계를 다루는 통계방법이다

  • LOWESS: 구간 촘촘하게 나눈 후 평균값
  • Cubic spline(cs): 구간 몇개로 나눈 후 각각 3차함수 fitting
  • Natural cubic spline(ns): cs 맨 처음과 끝구간만 선형 fitting
  • Smoothing spline(GAM default): 최적화때 smoothing penalty(\(\lambda\)) 부여

종속변수 형태따라 여러종류

  • Continuous: normal
  • Binary: logistic
  • Count: poisson, quasipoisson(평균 \(\neq\) 분산 일 때)
  • Survival: coxph

GAM theory

Non linear model

\[\begin{align} Y=\beta_0+\beta_1 x_{1}+\beta_2 x_2+\cdots+\epsilon \end{align}\] \[\begin{align} Y=\beta_0+ f(x_1)+\beta_2 x_2 \cdots+\epsilon \end{align}\] \(f(x_1,x_2)\)꼴의 형태도 가능

LOWESS

Locally weighted scatterplot smoothing

  • 구간 나눠 regression
  • 각 점마다 그 점을 포함하는 구간 설정
  • 가까운 점에 weight

LOWESS in ggplot

library(ggplot2);library(survival)
dd <- lapply(seq(0.1, 0.8, by = 0.2), function(span){
  ggplot(colon, aes(age, nodes)) + geom_point() + geom_smooth(method  = "loess", span = span) + ggtitle(paste0("Span =", span))
})

cowplot::plot_grid(plotlist = dd, nrow = 2)

Cubic spline

Cubic = 3차방정식

  • 구간을 몇 개로 나누고: knot
  • 각각을 3차함수로 fitting
  • 구간 사이 부드럽게 연결되도록 제한조건

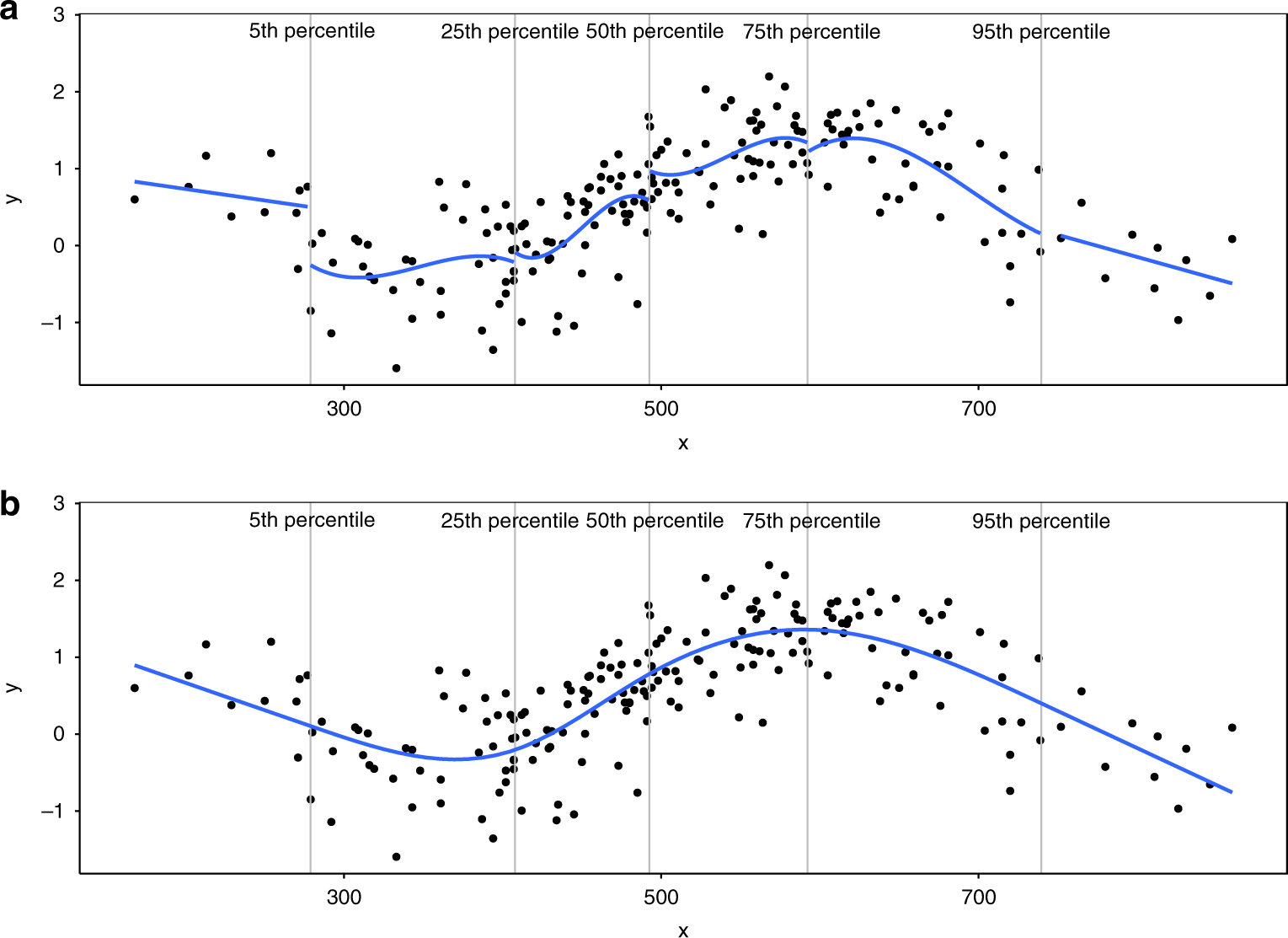
Natural cubic spline(ns)

Cubic + 처음과 끝은 Linear

  • 처음보다 더 처음, 끝보다 더 끝(데이터에 없는 숫자)에 대한 보수적인 추정.
  • 3차보다 1차가 변화량 적음.

Cubic spline in R

library(splines)
cs1 <- glm(time ~ bs(age, knots = c(40, 50, 60, 70)) + sex, data = colon)
cs2 <- glm(time ~ bs(age, df = 4) + sex, data = colon)
ns1 <- glm(time ~ ns(age, knots = c(40, 50, 60, 70)) + sex, data = colon)
ns2 <- glm(time ~ ns(age, df = 4) + sex, data = colon)

age.grid <- seq(min(colon$age), max(colon$age), by = 1)
with(colon, plot(age,time,col="grey",xlab="Age",ylab="Time"))
points(age.grid, predict(cs1, newdata = data.frame(age=age.grid, sex = 1)), col=1, lwd=1, type="l")
points(age.grid, predict(cs2, newdata = data.frame(age=age.grid, sex = 1)), col=2, lwd=2, type="l")
points(age.grid, predict(ns1, newdata = data.frame(age=age.grid, sex = 1)), col=3, lwd=3, type="l")
points(age.grid, predict(ns2, newdata = data.frame(age=age.grid, sex = 1)), col=4, lwd=4, type="l")
#adding cutpoints
abline(v = c(40, 50, 60, 70), lty=2, col="black")
legend("topleft", c("cs:knots" ,"cs:df", "ns:knots", "ns:df"), col = 1:4, lwd = 1:4)

Smoothing spline

mgcv R 패키지의 기본옵션.

Loess, Cubic spline

  • Span, knot를 미리 지정: local 구간을 미리 지정.

Smoothing(penalized) spline

  • 알아서.. 데이터가 말해주는 대로..

Penalized regression: Smoothing

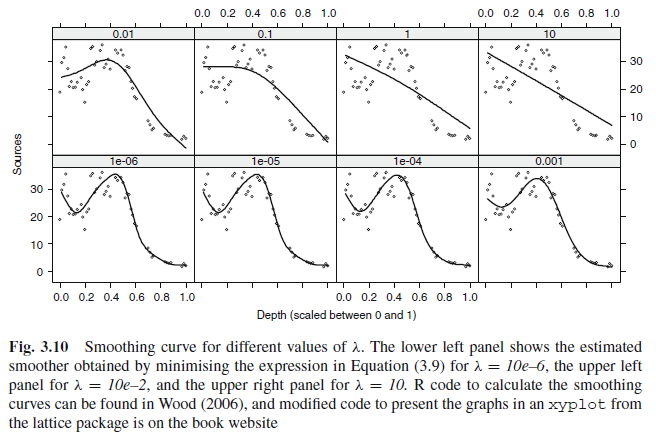
\[\begin{align*} \text{Minimize} ||Y - X\beta||^2 + \lambda \int f''(x)^2dx \end{align*}\]
  • \(\lambda\rightarrow 0\): 울퉁불퉁.
  • \(\lambda\)가 커질수록 smoothing
  • \(f''\) 는 기울기의 변화율, 제곱하면 절대값 의미

\(\lambda\)

Show gam result

  • edf(Effective df): 자유도 - shrinkage penalty
library(mgcv)
m1 <- gam(time ~ s(age) + sex, data = colon)
summary(m1)

Family: gaussian 
Link function: identity 

Formula:
time ~ s(age) + sex

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1533.194     31.619  48.489   <2e-16 ***
sex            8.354     43.851   0.191    0.849    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
         edf Ref.df     F p-value   
s(age) 7.584  8.447 2.725 0.00437 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.00938   Deviance explained =  1.4%
GCV = 8.9245e+05  Scale est. = 8.8784e+05  n = 1858
## Lambda
m1$sp
    s(age) 
0.04120719 
#m1 <- gam(time ~ s(age, sp = 0.04120719) + sex, data = colon)

Plot

plot(m1, shade = T)   ## plot(m1, select = 1)

Basis function

Smoothing spline: basis function 들의 합

\[s(x) = \sum_{k = 1}^K \beta_k b_k(x)\]

출처

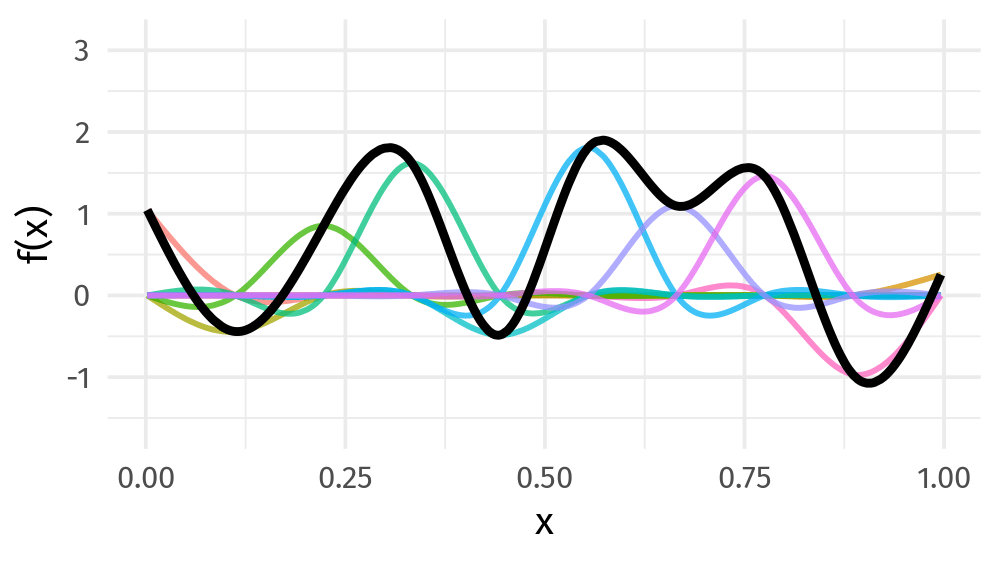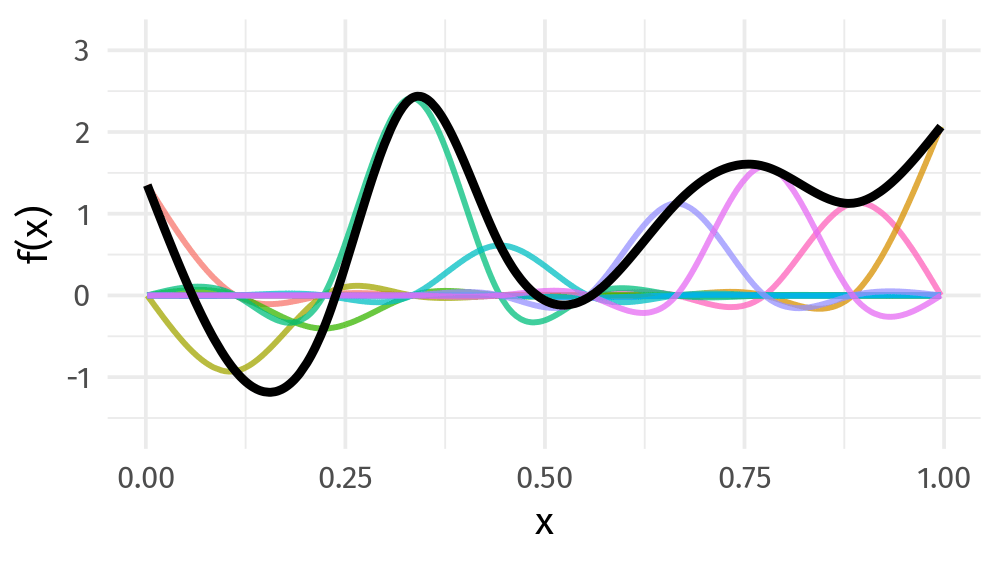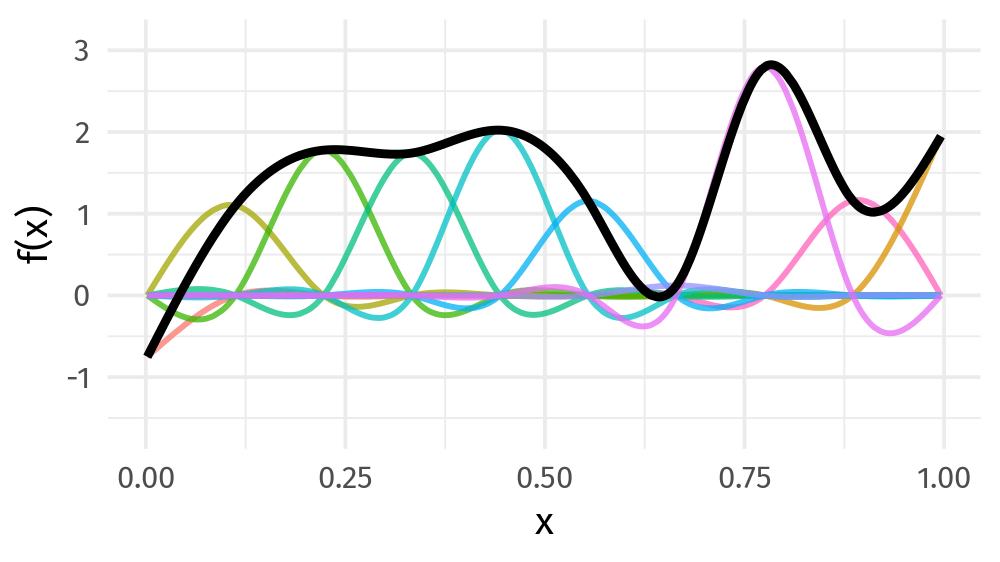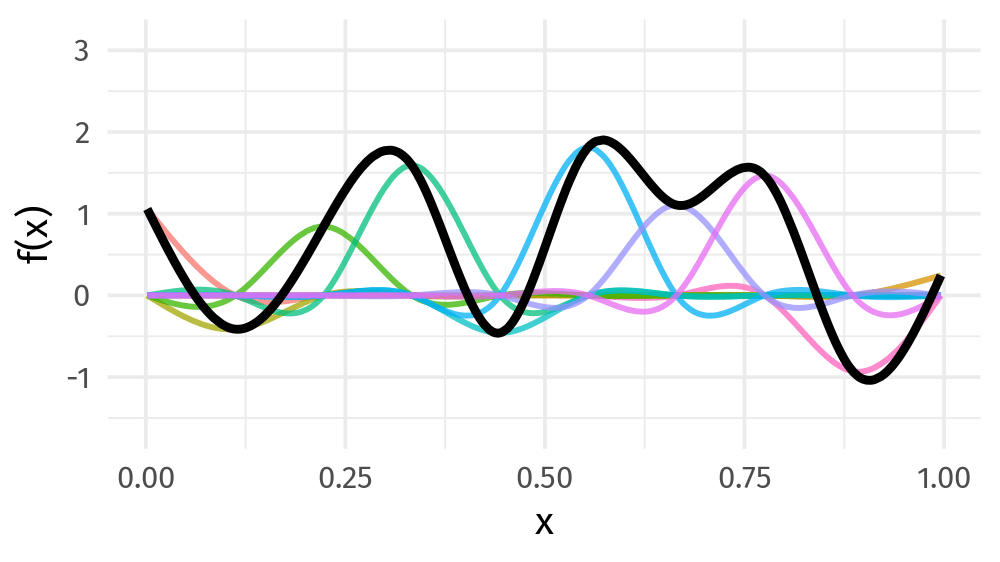
Basis function: value

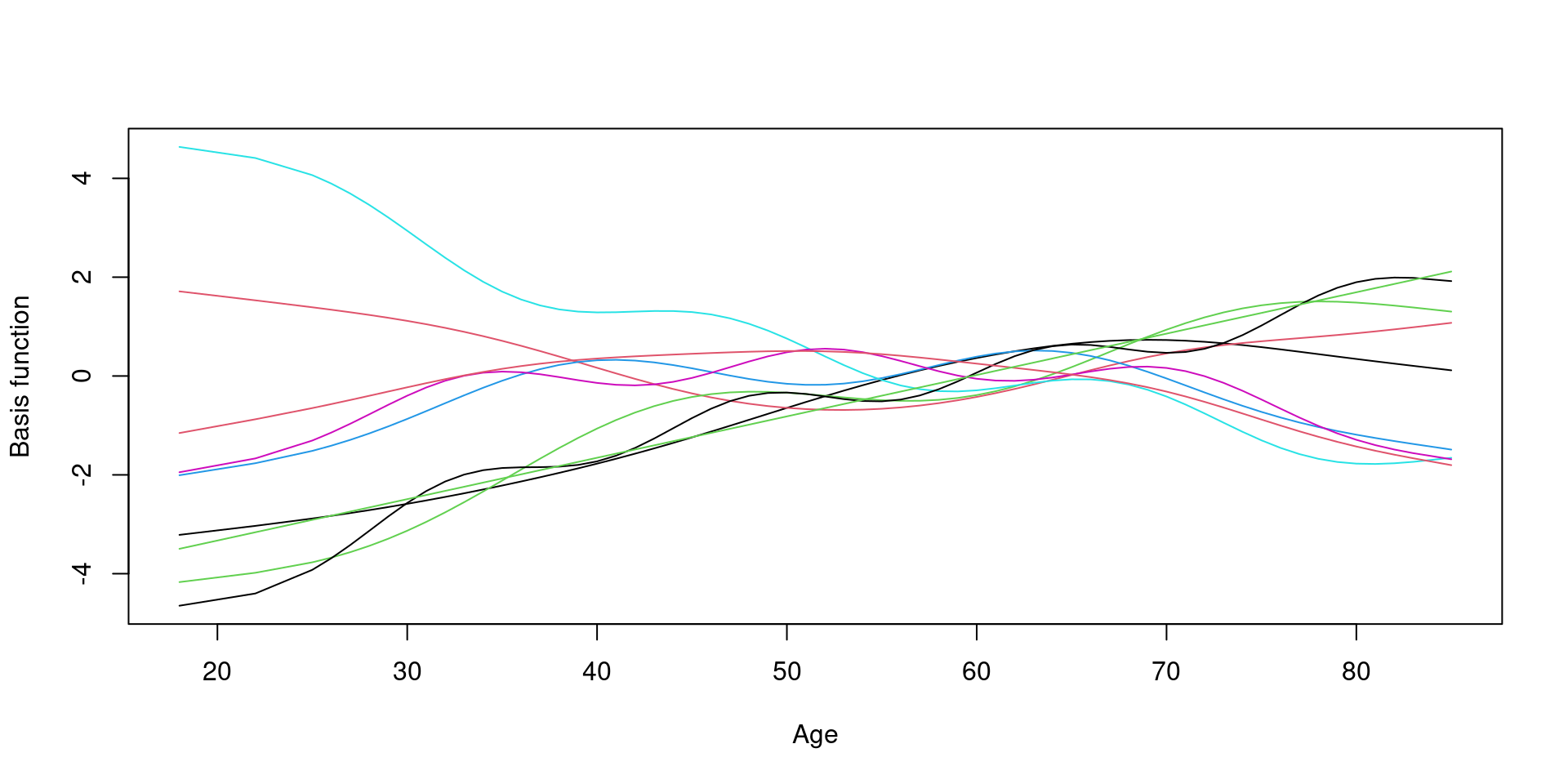
model_matrix <- predict(m1, type = "lpmatrix", newdata = data.frame(age = sort(colon$age), sex = 1))

DT::datatable(round(model_matrix, 2), rownames = F, options = list(scrollX = T,scrollCollapse = T))

Basis function: plot

9개의 basis function

matplot(sort(colon$age), model_matrix[,-c(1:2)], type = "l", lty = 1, xlab = "Age", ylab = "Basis function")

GAM result

model_matrix 에 계수를 곱하면 곡선의 y값

coef(m1)
 (Intercept)          sex     s(age).1     s(age).2     s(age).3     s(age).4 
 1533.193607     8.353593   776.245594  1393.793067   232.785846 -1154.982151 
    s(age).5     s(age).6     s(age).7     s(age).8     s(age).9 
 -324.817013 -1018.225598   274.926370  3106.242791  -783.531680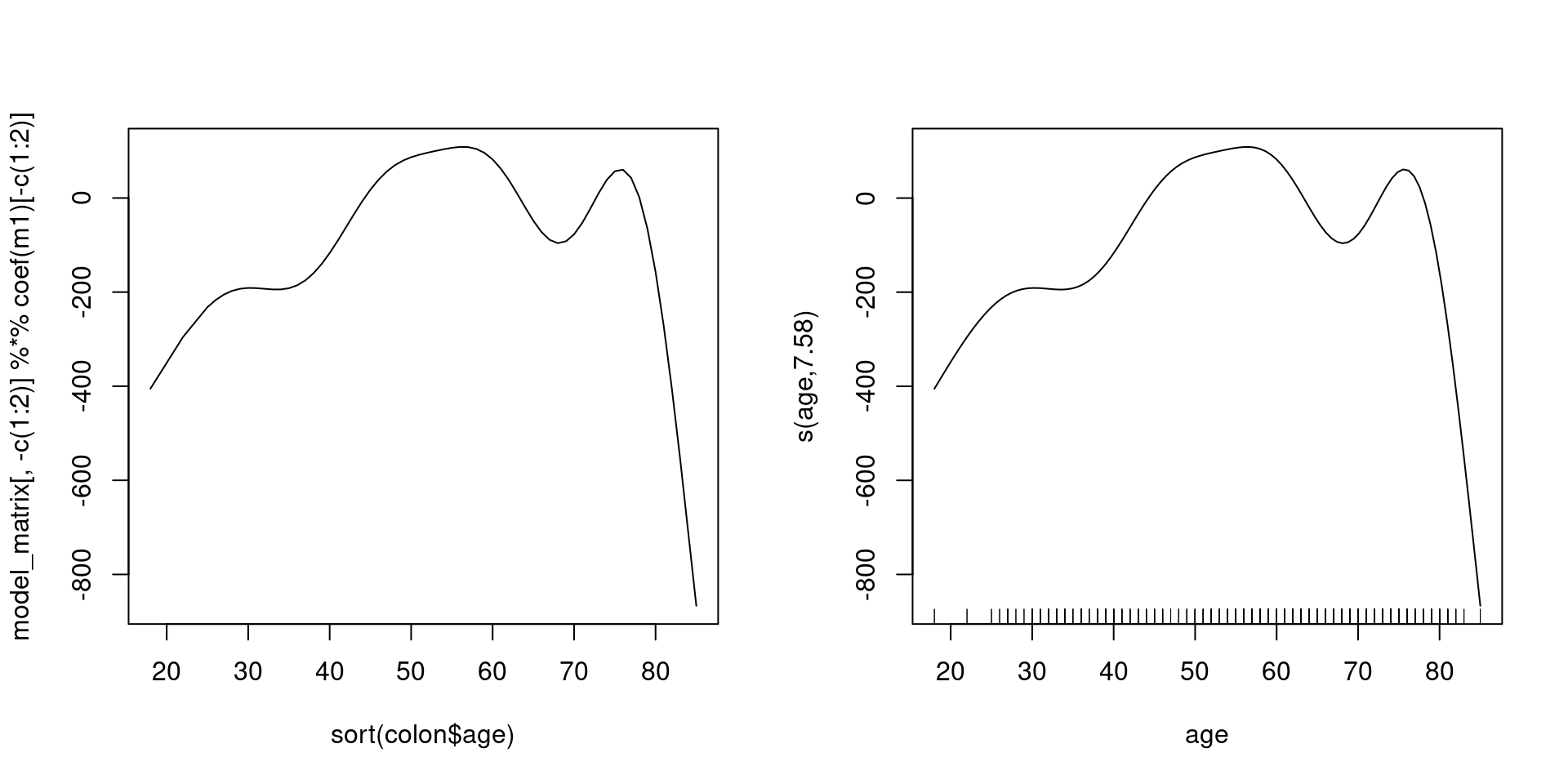 
par(mfrow = c(1, 2))
plot(sort(colon$age), model_matrix[,-c(1:2)] %*% coef(m1)[-c(1:2)], type = "l")
plot(m1, shade = T, se = F)   ## plot(m1, select = 1)

Change basis function

m2 <- gam(time ~ s(age, bs = "cr") + sex, data = colon)
model_matrix2 <- predict(m2, type = "lpmatrix", newdata = data.frame(age = sort(colon$age), sex = 1))
matplot(sort(colon$age), model_matrix2[,-c(1:2)], type = "l", lty = 1, xlab = "Age", ylab = "Basis function")

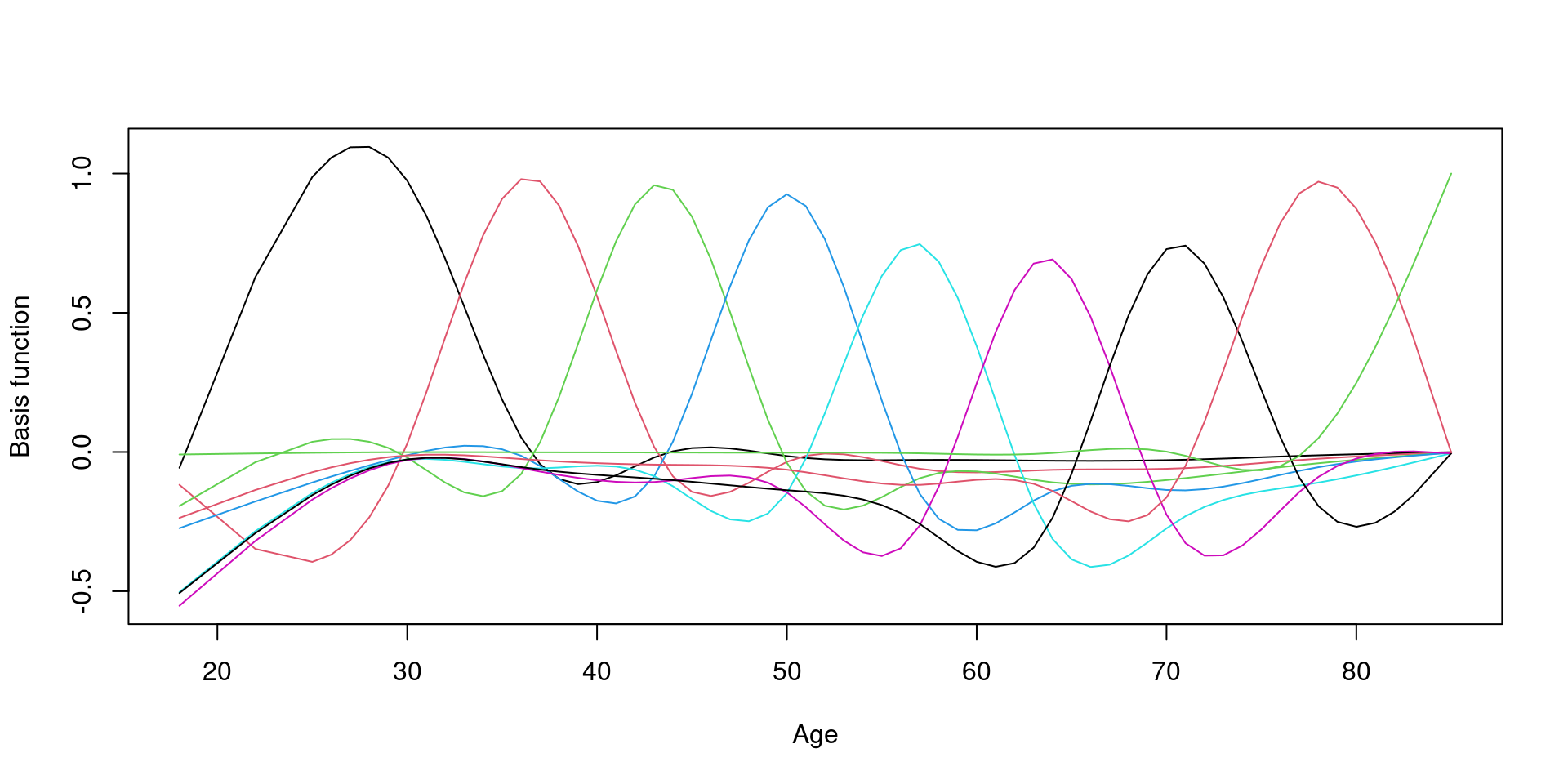
Restricted df

\(k = 6\): df의 최대값을 6으로 제한

m3 <- gam(time ~ s(age, bs = "cr", k = 6) + sex, data = colon)
model_matrix3 <- predict(m3, type = "lpmatrix", newdata = data.frame(age = sort(colon$age), sex = 1))
matplot(sort(colon$age), model_matrix3[,-c(1:2)], type = "l", lty = 1, xlab = "Age", ylab = "Basis function")

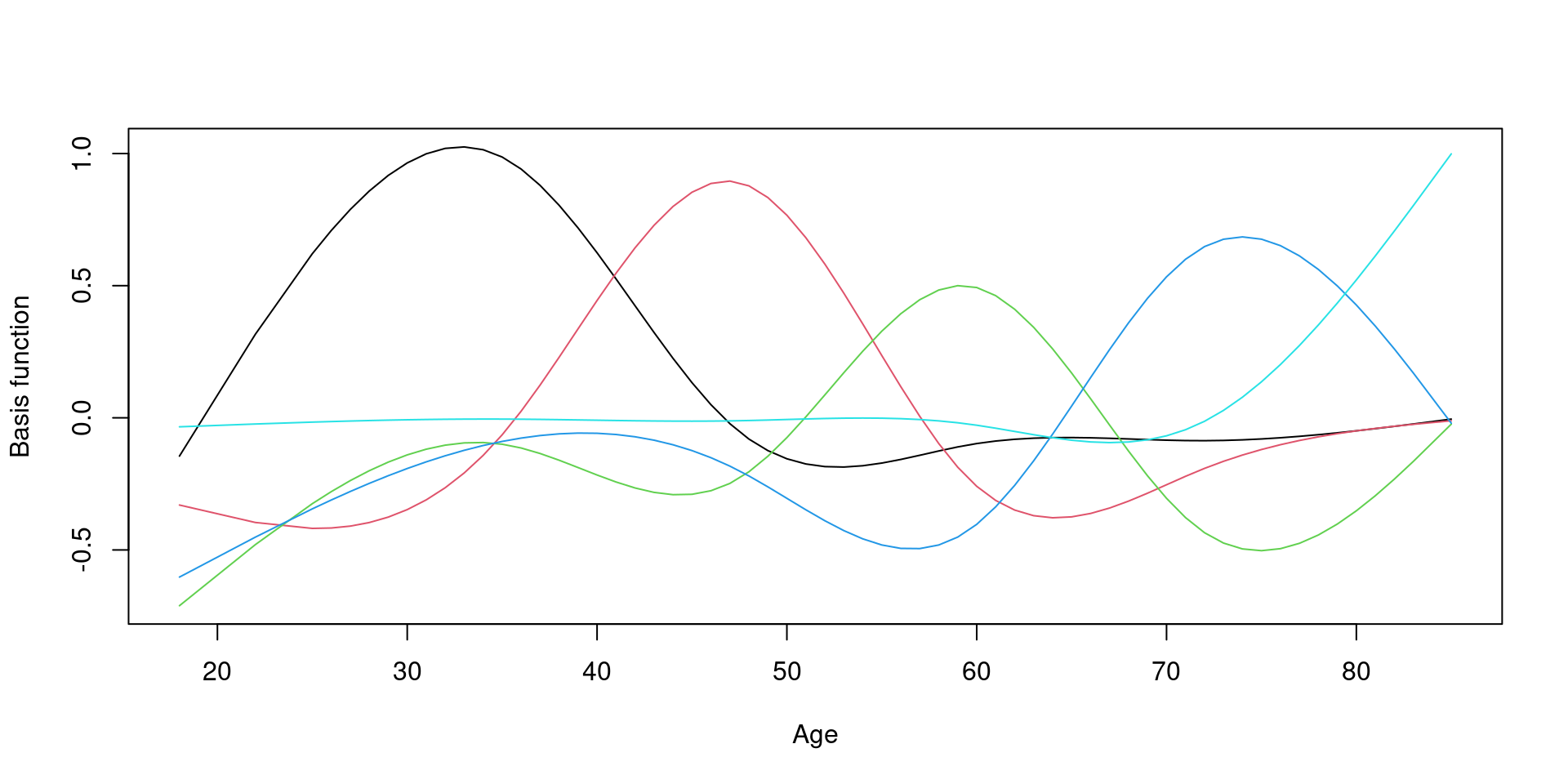
Fix \(\lambda\)

sp = 1000: \(\lambda\) 1000으로 고정, 거의 직선을 의미

m4 <- gam(time ~ s(age, sp = 1000) + sex, data = colon)
plot(m4)

Other distribution

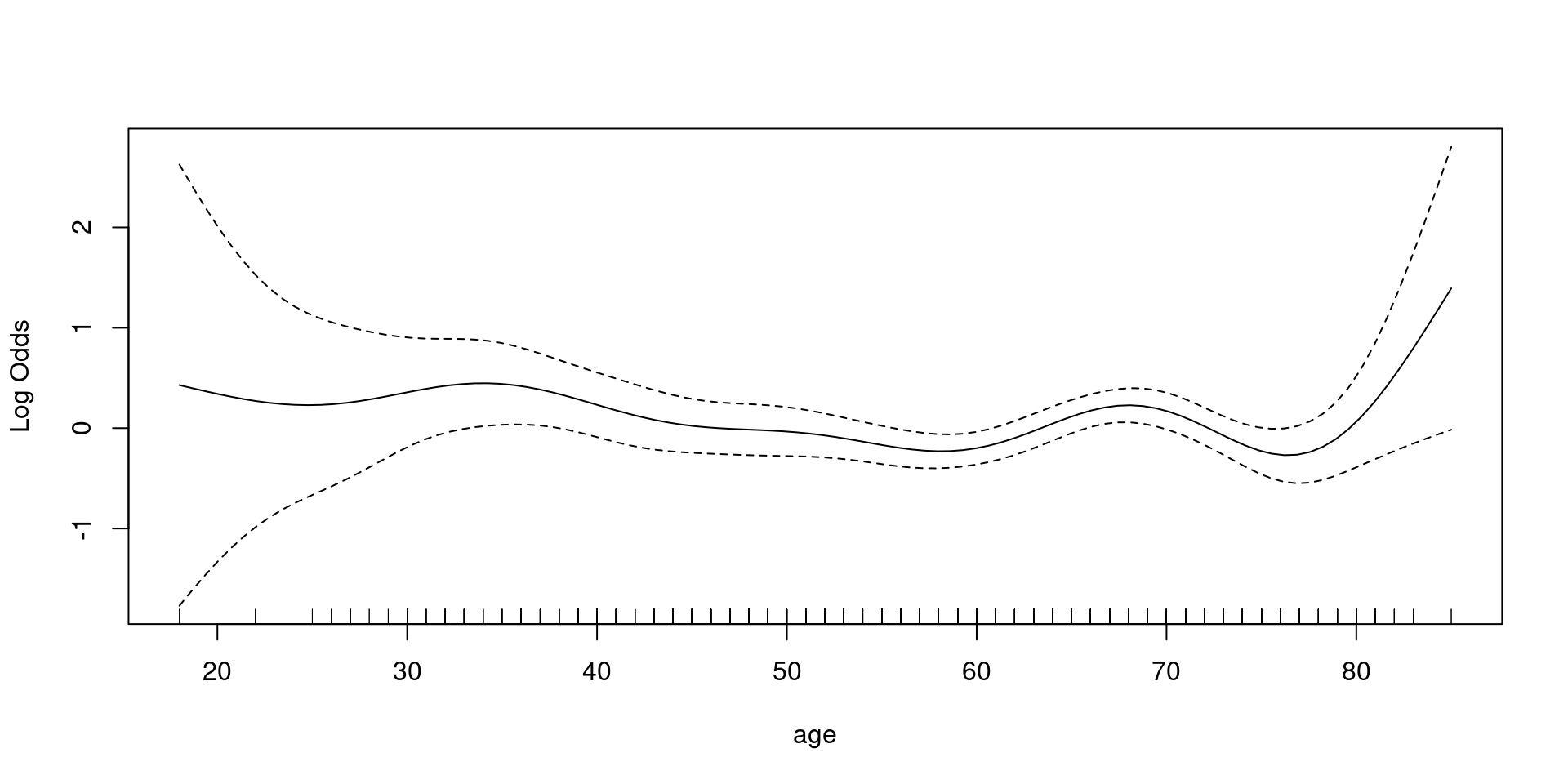
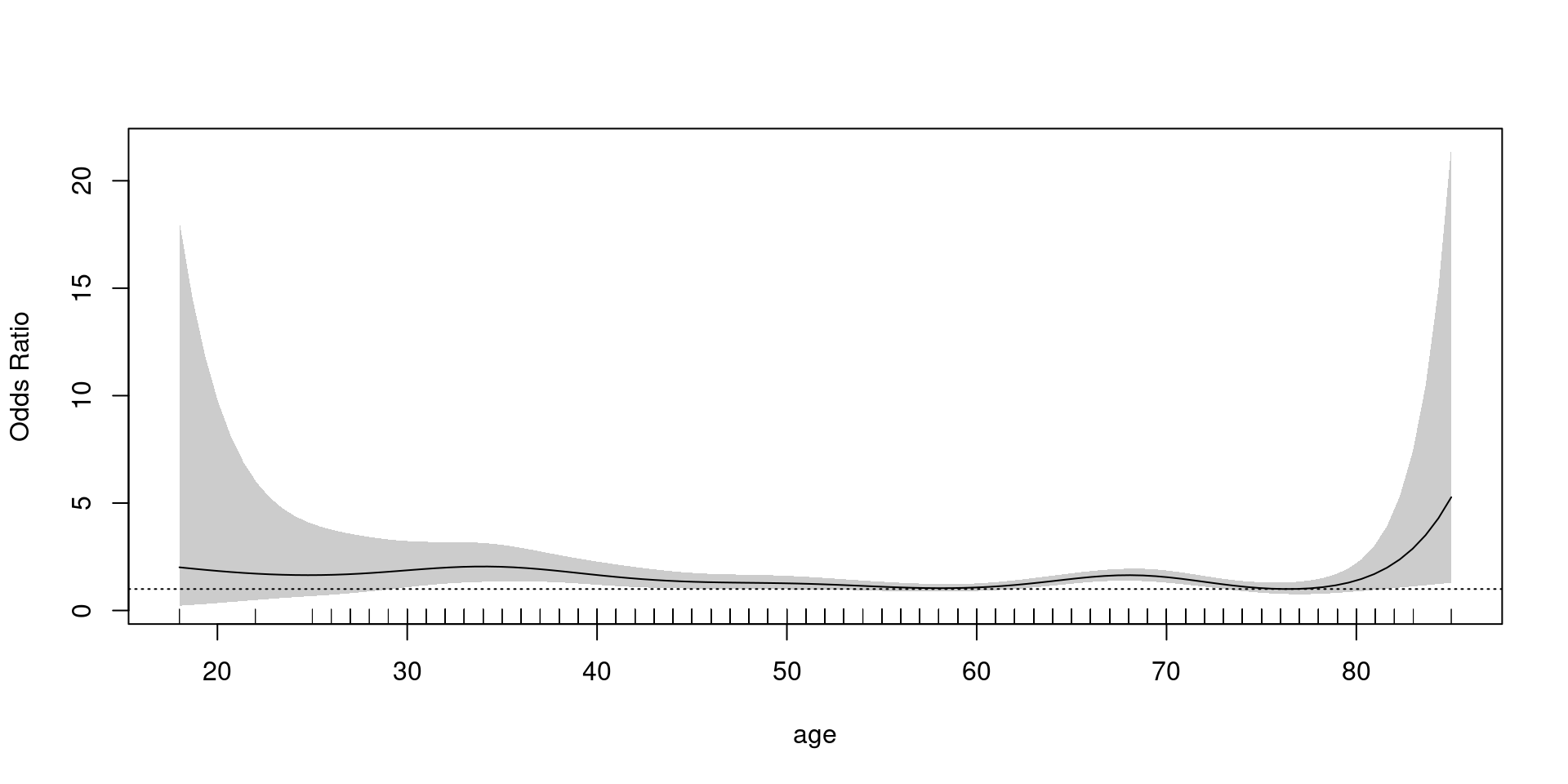
Logistic

family = binomial

  • 해석에 주의: log Odds
  • exponential transformation, reference(OR =1) 설정 필요
m5 <- gam(status ~ s(age) + sex, data = colon, family = binomial)
zz <- plot(m5, ylab = "Log Odds")

plot(m5, trans = exp, ylab = "Odds Ratio", shade = T, shift = -min(zz[[1]]$fit))
abline(h = 1, lty = 3)

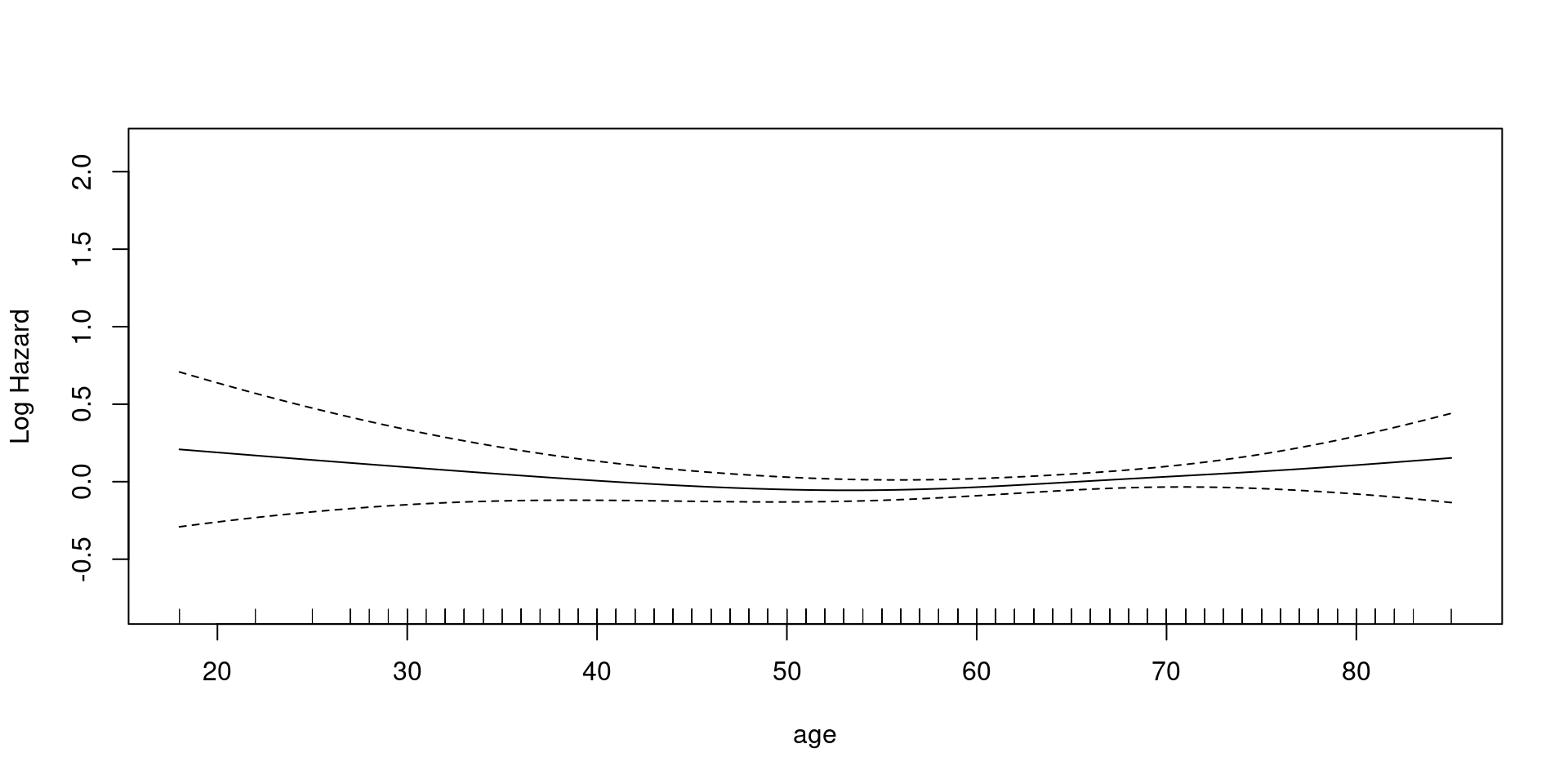
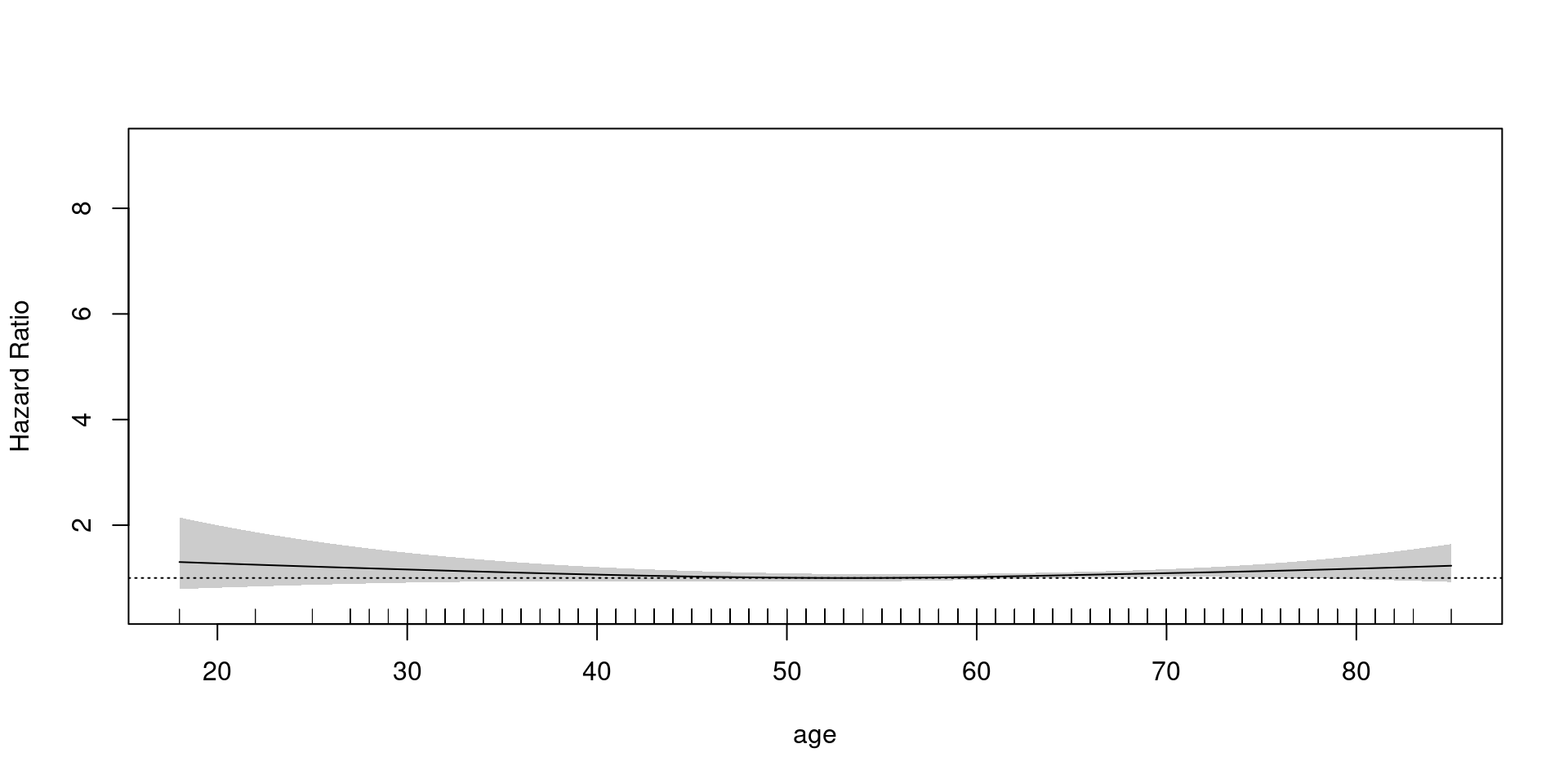
Coxph

family = cox.ph - weights = status

m6 <-  gam(time ~ s(age) + sex + s(nodes), family=cox.ph, data= colon, weights = status)
zz <- plot(m6, select = 1, ylab = "Log Hazard")

plot(m6, select = 1, trans = exp, ylab = "Hazard Ratio", shade = T, shift = -min(zz[[1]]$fit))
abline(h = 1, lty = 3)

Poisson

family = poisson - exp trans

mort <- read.csv("https://raw.githubusercontent.com/jinseob2kim/R-skku-biohrs/main/docs/gam/mort.csv")
m7 <- gam(nonacc ~ s(meanpm10) + s(meantemp), data = mort, family = poisson)
zz <- plot(m7, select = 1, ylab = "Log RR")

plot(m7, select = 1, trans = exp, ylab = "Risk Ratio", shade = T, shift = -min(zz[[1]]$fit))
abline(h = 1, lty = 3)

Quasi-poisson

Poisson 분포의 가정 평균=분산 이 만족하지 않을 때.

  • family = quasipoisson
  • \(평균 = \phi * 분산\)
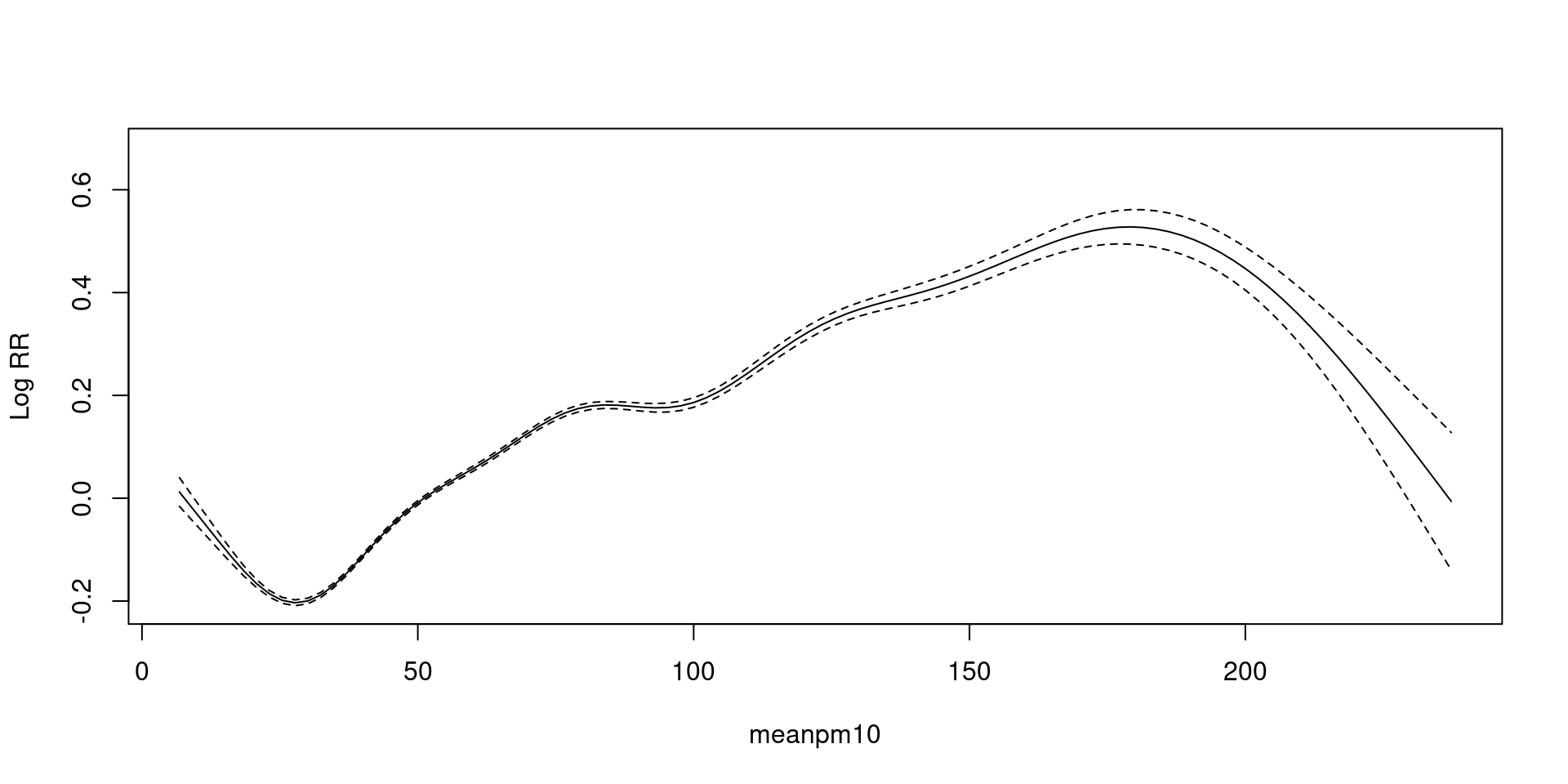
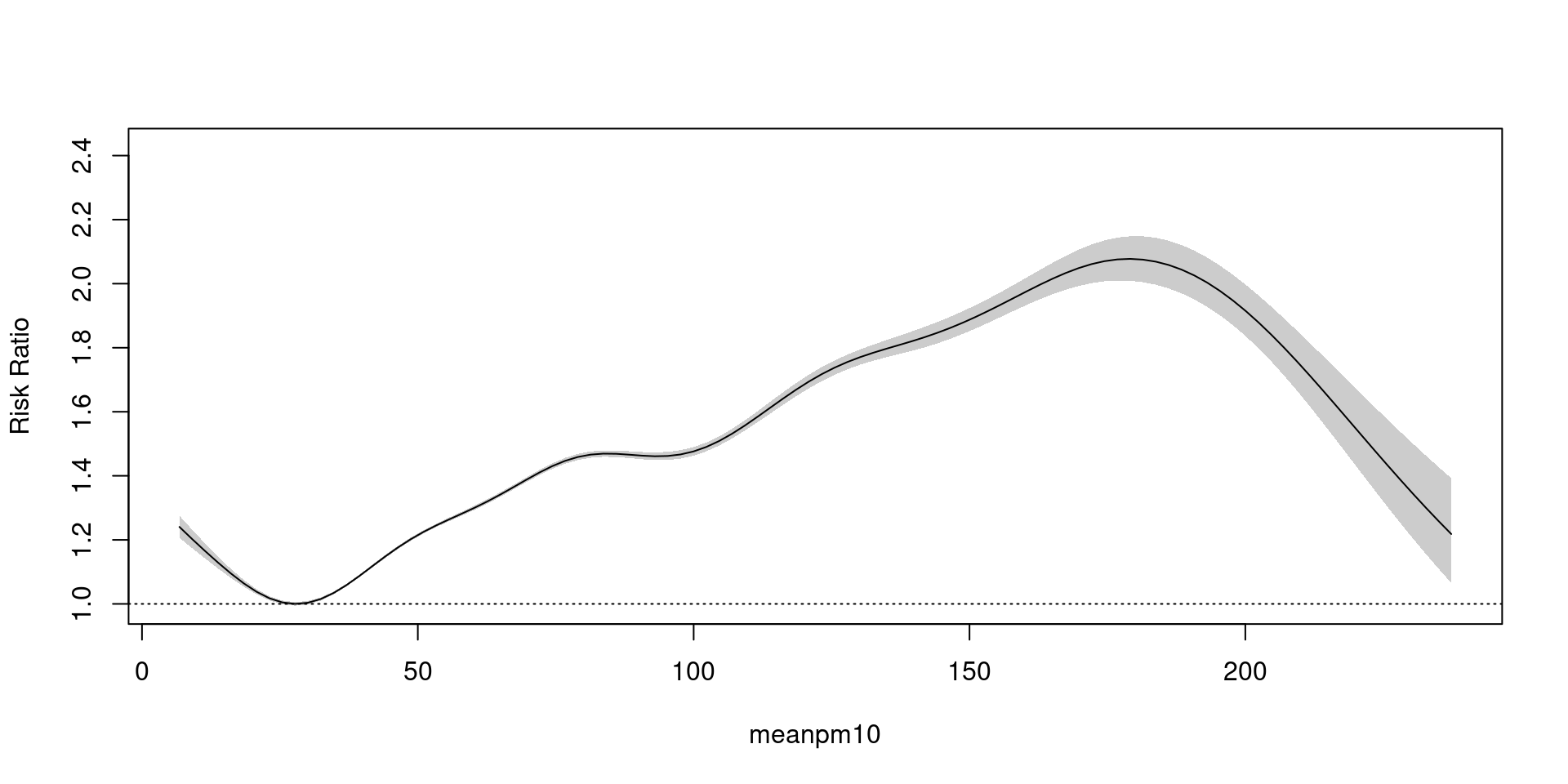
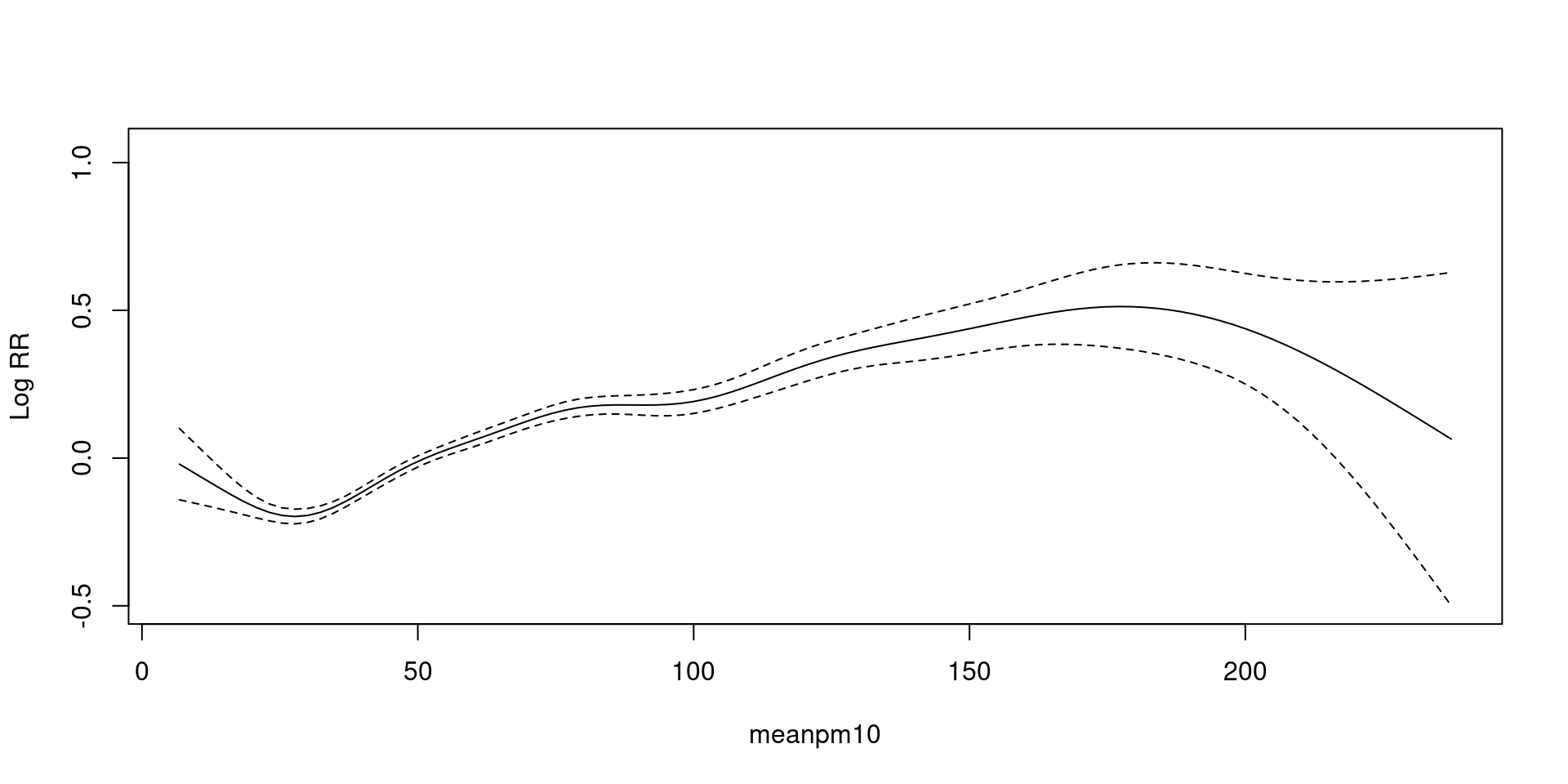
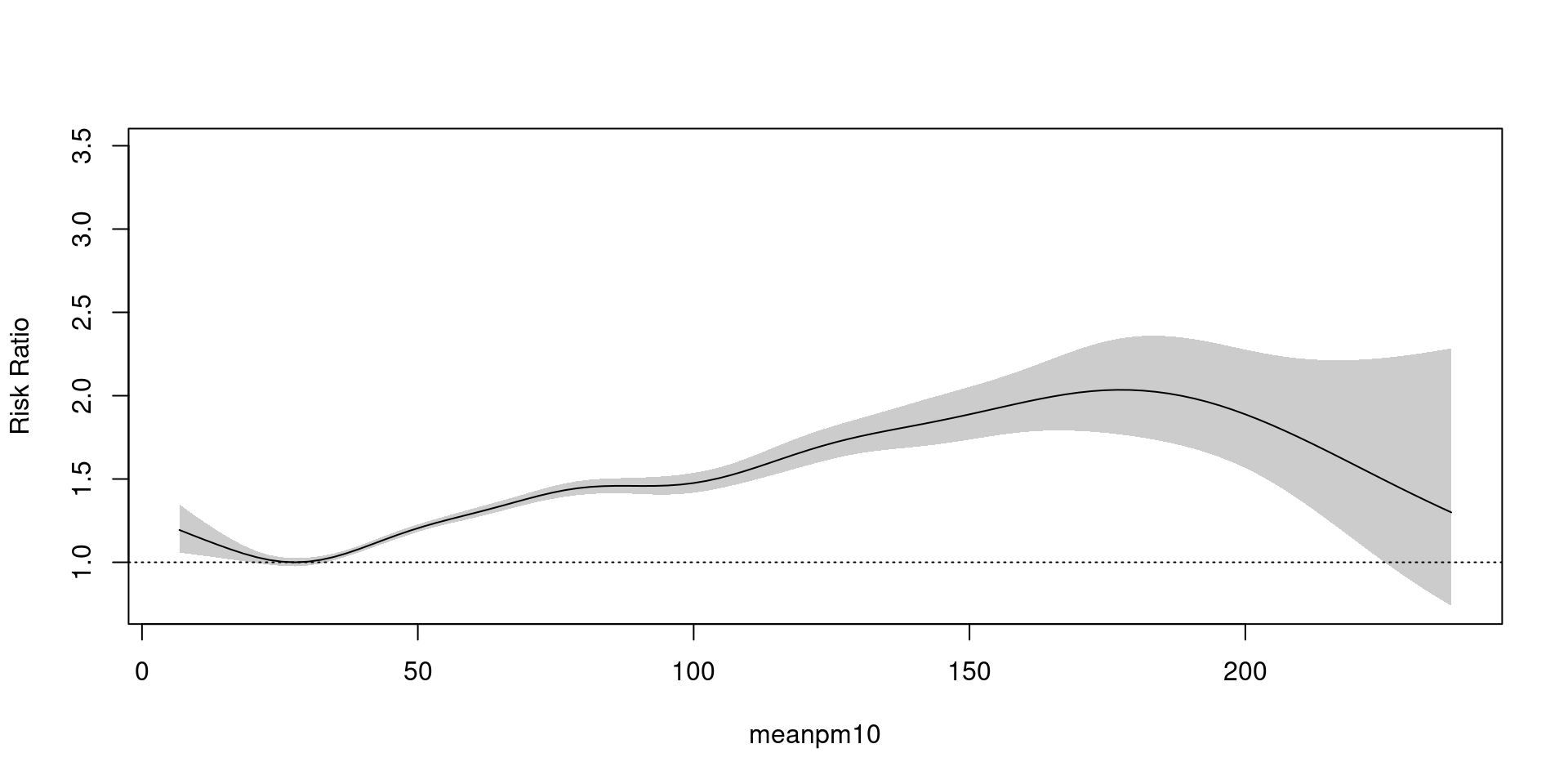
  • 곡선 자체는 그대로, 신뢰구간만 넓어짐(보수적 추정)
c(mean(mort$nonacc), var(mort$nonacc))
[1]  36.51577 797.91493
m7$scale.estimated
[1] FALSE
m8 <- gam(nonacc ~ s(meanpm10) + s(meantemp), data = mort, family = quasipoisson)
zz <- plot(m8, select = 1, ylab = "Log RR")

plot(m8, select = 1, trans = exp, ylab = "Risk Ratio", shade = T, shift = -min(zz[[1]]$fit))
abline(h = 1, lty = 3)

Thank you for your time

www.zarathu.com